



suivant: 3.2.3.4 d. K :
monter: 3.2.3 Cas de l'expérience
précédent: 3.2.3.2 b. Etats absolument
Table des matières
Que se passe-t-il si nous diminuons la contrainte  ? Nous
présentons maintenant le régime intermédiaire entre le voisinage
du premier seuil -- où les ondes sont stables d'Eckhaus -- et le
régime absolument instable d'Eckhaus -- au delà de 5,56 K. Dans ce
régime intermédiaire, les comportements sont beaucoup plus
diversifiés.
? Nous
présentons maintenant le régime intermédiaire entre le voisinage
du premier seuil -- où les ondes sont stables d'Eckhaus -- et le
régime absolument instable d'Eckhaus -- au delà de 5,56 K. Dans ce
régime intermédiaire, les comportements sont beaucoup plus
diversifiés.
La figure ![[*]](crossref.png) illustre un premier cas simple
d'instablité convective où une perturbation initiale nourrit pendant
de nombreuses périodes une modulation qui est petit à petit
advectée vers l'aval par la vitesse de groupe. Le système relaxe
donc vers un état uniforme, sans modulation. Dans ce régime, les
ondes sont instables d'Eckhaus, mais le taux de croissance temporel des
modulations est négatif et il est impossible de définir une position
stationnaire du front des dislocations. Celui-ci n'existe que lors de
périodes transitoires ; par exemple après une perturbation
mécanique du système (ajout d'une goutte d'huile) ou bien un
changement de
illustre un premier cas simple
d'instablité convective où une perturbation initiale nourrit pendant
de nombreuses périodes une modulation qui est petit à petit
advectée vers l'aval par la vitesse de groupe. Le système relaxe
donc vers un état uniforme, sans modulation. Dans ce régime, les
ondes sont instables d'Eckhaus, mais le taux de croissance temporel des
modulations est négatif et il est impossible de définir une position
stationnaire du front des dislocations. Celui-ci n'existe que lors de
périodes transitoires ; par exemple après une perturbation
mécanique du système (ajout d'une goutte d'huile) ou bien un
changement de  .
.
Figure:
Instabilité d'Eckhaus convective.
Diagrammes spatio-temporels du nombre d'onde local instantané
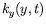 dans le rectangle pour
dans le rectangle pour
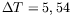 K (en haut)
et
K (en haut)
et
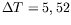 K (en bas).
A gauche sont reproduits les signaux
K (en bas).
A gauche sont reproduits les signaux
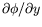 et
à droite les amplitudes des modulations de nombre d'onde telles
que données par une transformée de Hilbert en temps.
Les diagrammes de gauche révèlent clairement que la zone 21
est instable : l'amplitude de la modulation est croissante en
espace et décroissante en temps ; l'instabilité est convective.
et
à droite les amplitudes des modulations de nombre d'onde telles
que données par une transformée de Hilbert en temps.
Les diagrammes de gauche révèlent clairement que la zone 21
est instable : l'amplitude de la modulation est croissante en
espace et décroissante en temps ; l'instabilité est convective.
|
|
Nous pouvons néanmoins définir un taux de croissance spatial
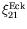 . Ce dernier est positif au delà d'une certaine valeur
. Ce dernier est positif au delà d'une certaine valeur
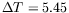 K, ce qui confirme la notion d'instabilité d'Eckhaus
même si le front est évacué hors de la cellule. La dépendance de
K, ce qui confirme la notion d'instabilité d'Eckhaus
même si le front est évacué hors de la cellule. La dépendance de
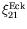 vis à vis de
vis à vis de  est reproduite sur la
figure
est reproduite sur la
figure ![[*]](crossref.png) . Ce taux de croissance spatial tend vers
zéro quand
. Ce taux de croissance spatial tend vers
zéro quand
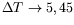 K par valeurs supérieures.
K par valeurs supérieures.
Figure:
Variation du taux de croissance spatial, en fonction de  ,
mesuré sur des états de relaxation (symboles
,
mesuré sur des états de relaxation (symboles 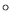 ).
).
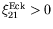 signe des états instables.
Les points de la zone d'instabilité d'Eckhaus absolue
(symboles
signe des états instables.
Les points de la zone d'instabilité d'Eckhaus absolue
(symboles  ) sont reproduits pour comparaison.
) sont reproduits pour comparaison.
|
|
Remarquons que les états décrits jusqu'à présent étaient
caractérisés par la relaxation d'une perturbation forte (remplissage
typiquement) ou bien par diminution de  à partir d'un état
absolument instable d'Eckhaus. Nous pouvons en cela les appeller des
états fortement non-linéaires.
à partir d'un état
absolument instable d'Eckhaus. Nous pouvons en cela les appeller des
états fortement non-linéaires.




suivant: 3.2.3.4 d. K :
monter: 3.2.3 Cas de l'expérience
précédent: 3.2.3.2 b. Etats absolument
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) illustre un premier cas simple
d'instablité convective où une perturbation initiale nourrit pendant
de nombreuses périodes une modulation qui est petit à petit
advectée vers l'aval par la vitesse de groupe. Le système relaxe
donc vers un état uniforme, sans modulation. Dans ce régime, les
ondes sont instables d'Eckhaus, mais le taux de croissance temporel des
modulations est négatif et il est impossible de définir une position
stationnaire du front des dislocations. Celui-ci n'existe que lors de
périodes transitoires ; par exemple après une perturbation
mécanique du système (ajout d'une goutte d'huile) ou bien un
changement de
illustre un premier cas simple
d'instablité convective où une perturbation initiale nourrit pendant
de nombreuses périodes une modulation qui est petit à petit
advectée vers l'aval par la vitesse de groupe. Le système relaxe
donc vers un état uniforme, sans modulation. Dans ce régime, les
ondes sont instables d'Eckhaus, mais le taux de croissance temporel des
modulations est négatif et il est impossible de définir une position
stationnaire du front des dislocations. Celui-ci n'existe que lors de
périodes transitoires ; par exemple après une perturbation
mécanique du système (ajout d'une goutte d'huile) ou bien un
changement de ![]() .
.
![\includegraphics[width=7.5cm]{b01dkx}](img885.png)
![\includegraphics[width=7.5cm]{b01dkxf}](img886.png)
![\includegraphics[width=7.5cm]{a27ekx}](img887.png)
![\includegraphics[width=7.5cm]{a27ekxf}](img888.png)
![]() . Ce dernier est positif au delà d'une certaine valeur
. Ce dernier est positif au delà d'une certaine valeur
![]() K, ce qui confirme la notion d'instabilité d'Eckhaus
même si le front est évacué hors de la cellule. La dépendance de
K, ce qui confirme la notion d'instabilité d'Eckhaus
même si le front est évacué hors de la cellule. La dépendance de
![]() vis à vis de
vis à vis de ![]() est reproduite sur la
figure
est reproduite sur la
figure ![[*]](crossref.png) . Ce taux de croissance spatial tend vers
zéro quand
. Ce taux de croissance spatial tend vers
zéro quand
![]() K par valeurs supérieures.
K par valeurs supérieures.
![\includegraphics[width=8cm]{xi-eck-b}](img893.png)