



suivant: 4.2.6.2 Un phénomène uniquement
monter: 4.2.6 Commentaires et conclusions
précédent: 4.2.6 Commentaires et conclusions
Table des matières
La géométrie étudiée -- cylindrique -- nous conduit à des
résultats tout à fait dissymétriques lorsque côté chaud et
côté froid sont intervertis. Cela provient de la présence de
nouveaux termes -- dus à la courbure -- dans les équations
régissant les mouvements du fluide. Ces termes ne sont pas
symétriques sous la transformation
 qui
accompagne un changement de signe de
qui
accompagne un changement de signe de  .
.
A notre connaissance, aucun résultat expérimental précis n'existe
à ce jour en géométrie cartésienne (rectangle) sur l'évolution
de l'amplitude et la propagation du front des rouleaux stationnnaires.
Nous pouvons néanmoins déduire de nos résultats en géométrie
cylindrique que :
- Les rouleaux apparaissent préférentiellement pour les plus
grandes hauteurs de fluide (
 mm est plus favorable que
mm est plus favorable que
 mm) . Ce résultat déjà connu de Pelacho et Burguete (1999) est
confirmé.
mm) . Ce résultat déjà connu de Pelacho et Burguete (1999) est
confirmé.
- Les rouleaux apparaissent toujours du côté chaud pour l'huile
utilisée (
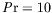 ), et envahissent ensuite progressivement la
cellule ; un taux de croissance spatial est donc attaché à cette
structure.
), et envahissent ensuite progressivement la
cellule ; un taux de croissance spatial est donc attaché à cette
structure.
- Il est possible de définir, à l'
 il, un seuil pour
l'apparition des rouleaux. Ceci est indiscutable dans le cas
il, un seuil pour
l'apparition des rouleaux. Ceci est indiscutable dans le cas
 , et semble aussi très probable pour
, et semble aussi très probable pour
 .
.
- Le seuil d'apparition des rouleaux précède celui des ondes
hydrothermales OH1 (ainsi que celui d'un autre mode oscillant : les
fleurs).
De précédents travaux (Mercier et Normand (2000)) prédisent par ailleurs
que cet effet des bords latéraux est accompagné d'un taux de
croissance spatial. A partir des profils d'amplitude locale, nous avons
cherché à définir un tel taux de croissance spatial.
Malheureusement, la variation de l'amplitude n'est pas exponentielle,
mais plutôt linéaire, et nous n'avons pu définir une telle
grandeur. En fait, les effets de courbure se superposent aux effets
d'amortissement spatial et tout ajustement quantitatif doit tenir compte
des deux effets.
Mais si nous ajoutons qualitativement aux effets de courbure l'effet de
la localisation spatiale, nous pouvons interpréter comme suit nos
observations :
-
 , i.e.,
, i.e.,
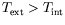 : les
rouleaux poussent tout d'abord du coté chaud à l'extérieur, mais
la longueur de pénétration est faible à cause des effets
(contraires) de la courbure. Tant que cette longueur de pénétration
est inférieure à une fraction de la longueur d'onde, aucun rouleau
ne peut être observé. Lorsque
: les
rouleaux poussent tout d'abord du coté chaud à l'extérieur, mais
la longueur de pénétration est faible à cause des effets
(contraires) de la courbure. Tant que cette longueur de pénétration
est inférieure à une fraction de la longueur d'onde, aucun rouleau
ne peut être observé. Lorsque  est assez élevée (au
delà de 8,5 K), la longueur de pénétration est de l'ordre de la
longuer d'onde et un rouleau est observé. Lorsque
est assez élevée (au
delà de 8,5 K), la longueur de pénétration est de l'ordre de la
longuer d'onde et un rouleau est observé. Lorsque  est plus
élevée encore (au delà de 10,2 K), le taux de croissance spatial
est assez fort pour contrer les effets de courbure loin du centre et les
rouleaux envahissent toute la cellule, le paramètre de contrôle
local étant plus fort au centre. Cette transition est brutale. Les
effets de courbure dominent alors et la structure est essentiellement
localisée au centre (bien qu'envahissant toute l'extension radiale).
est plus
élevée encore (au delà de 10,2 K), le taux de croissance spatial
est assez fort pour contrer les effets de courbure loin du centre et les
rouleaux envahissent toute la cellule, le paramètre de contrôle
local étant plus fort au centre. Cette transition est brutale. Les
effets de courbure dominent alors et la structure est essentiellement
localisée au centre (bien qu'envahissant toute l'extension radiale).
-
 , i.e.,
, i.e.,
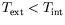 : les rouleaux
poussent tout d'abord du côté chaud, à l'intérieur. Cette
configuration est favorisée par un gradient horizontal local de
température plus élevé au centre à cause de la courbure.
La structure est donc toujours localisée au centre et elle envahit
progressivement la cellule lorsque
: les rouleaux
poussent tout d'abord du côté chaud, à l'intérieur. Cette
configuration est favorisée par un gradient horizontal local de
température plus élevé au centre à cause de la courbure.
La structure est donc toujours localisée au centre et elle envahit
progressivement la cellule lorsque
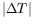 est augmenté. Il est
alors possible de définir un front du mode rouleaux.
est augmenté. Il est
alors possible de définir un front du mode rouleaux.




suivant: 4.2.6.2 Un phénomène uniquement
monter: 4.2.6 Commentaires et conclusions
précédent: 4.2.6 Commentaires et conclusions
Table des matières
Nicolas Garnier - Thèse de doctorat