



suivant: 5.4.2 Angles de propagation
monter: 5.4 Interprétations en termes
précédent: 5.4 Interprétations en termes
Table des matières
Nous allons ici montrer l'analogie de dénomination « OH1 » entre les
ondes hydrothermales observées dans le disque et celles observées
dans le rectangle, en la justifiant grâce à des arguments
géométiques.
Pour cela, nous représentons différemment les équiphases des ondes
obtenues sur un cliché ombroscopique. Comme expliqué dans
l'annexe ![[*]](crossref.png) , nous quittons la représentation de
l'espace réel pour nous placer dans le plan orthogonal
, nous quittons la représentation de
l'espace réel pour nous placer dans le plan orthogonal
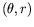 ,
i.e., dans un espace cartésien où la direction du gradient de
température et sa direction orthogonale locale se retrouvent
perpendiculaires en chaque point. La figure
,
i.e., dans un espace cartésien où la direction du gradient de
température et sa direction orthogonale locale se retrouvent
perpendiculaires en chaque point. La figure ![[*]](crossref.png) illustre cette transformation et permet d'affirmer qu'au premier ordre
les équiphases des OH1 relient
illustre cette transformation et permet d'affirmer qu'au premier ordre
les équiphases des OH1 relient 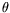 et
et 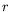 par une relation affine
et que ce sont donc des spirales d'Archimède. Le facteur de
proportionnalité est relié à l'angle de propagation par :
par une relation affine
et que ce sont donc des spirales d'Archimède. Le facteur de
proportionnalité est relié à l'angle de propagation par :
Figure:
Spirale unique d'OH1 obtenue pour  mm et
mm et
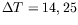 K.
A droite : cliché ombroscopique.
A gauche : sa représentation dans le plan orthogonal
K.
A droite : cliché ombroscopique.
A gauche : sa représentation dans le plan orthogonal
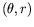 .
Nous en déduisons
.
Nous en déduisons
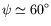 dans toute la cellule.
dans toute la cellule.
(360,140)
\linethickness{0.5pt}...
...0){\vector(0,1){20}}
\put(280,152){\makebox(0,0)[b]{$\vec{e}_r$}}
\end{picture}](img1148.png) |
Le fait que 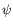 soit homogène partout dans la cellule et constant
vis à vis de
soit homogène partout dans la cellule et constant
vis à vis de  est bien la signature des ondes OH1 telles que
nous les avions définies en §
est bien la signature des ondes OH1 telles que
nous les avions définies en § ![[*]](crossref.png) .
.
Au contraire, dans le cas d'une OH2, l'angle 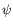 n'est pas homogène
dans la cellule ni constant vis-à-vis de
n'est pas homogène
dans la cellule ni constant vis-à-vis de  . La
figure
. La
figure ![[*]](crossref.png) présente ce cas. Nous y voyons
clairement que la source d'ondes émet des ondes cylindriques, tout comme
dans le cas du rectangle.
présente ce cas. Nous y voyons
clairement que la source d'ondes émet des ondes cylindriques, tout comme
dans le cas du rectangle.




suivant: 5.4.2 Angles de propagation
monter: 5.4 Interprétations en termes
précédent: 5.4 Interprétations en termes
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) , nous quittons la représentation de
l'espace réel pour nous placer dans le plan orthogonal
, nous quittons la représentation de
l'espace réel pour nous placer dans le plan orthogonal
![[*]](crossref.png) illustre cette transformation et permet d'affirmer qu'au premier ordre
les équiphases des OH1 relient
illustre cette transformation et permet d'affirmer qu'au premier ordre
les équiphases des OH1 relient ![\includegraphics[width=7cm]{0322-d30}](img1052.png)
![\includegraphics[width=7cm,height=3.5cm]{0322d30u}](img1147.png)
![\includegraphics[width=7cm,height=3.5cm]{0412c03u}](img1150.png)
![\includegraphics[width=7cm,height=3.5cm]{0412c33u}](img1151.png)
![\includegraphics[width=7cm,height=3.5cm]{0412c73u}](img1152.png)
![\includegraphics[width=7cm,height=3.5cm]{0412d12u}](img1153.png)