



suivant: 5.4.3 Rapports d'aspect et
monter: 5.4 Interprétations en termes
précédent: 5.4.1 Spirales d'Archimède
Table des matières
A partir des images dépliées comme en Fig. ![[*]](crossref.png) ,
nous pouvons non seulement discerner qualitativement entre OH1 et OH2,
mais aussi quantifier l'angle de propagation
,
nous pouvons non seulement discerner qualitativement entre OH1 et OH2,
mais aussi quantifier l'angle de propagation 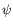 .
.
En résumé, nous avons qualitativement :
| ondes OH1 |
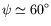 |
| ondes OH2 |
 au seuil au seuil |
| |
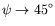 pour pour  croissant croissant |
| ondes fleurs |
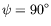 |
| ondes rayons |
 |
Sachant que le nombre de Prantdl est fixé, quelle richesse
insoupçonnée ! Mais comme nous l'avons trouvé analytiquement et
numériquement, la courbure peut modifier l'angle de propagation des
ondes au seuil. Nous pouvons même, à la lumière des résultats de
la section § ![[*]](crossref.png) , proposer le petit scénario suivant
pour l'évolution avec
, proposer le petit scénario suivant
pour l'évolution avec  de la structure spatiale des OH2 :
de la structure spatiale des OH2 :
Pour
 , le seuil est plus faible pour les plus fortes
courbures
, le seuil est plus faible pour les plus fortes
courbures 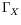 , réalisées près du plot central. Les ondes
apparaissent donc au centre et elles y sont localisées car seule une
région centrale est supercritique grâce à la courbure. Toujours
à cause de la courbure plus forte, le vecteur d'onde critique est
celui où le nombre d'onde orthoradial est nul (si la courbure est
assez forte). Nous avons ainsi au seuil des cibles pulsantes
localisées. Lorsque
, réalisées près du plot central. Les ondes
apparaissent donc au centre et elles y sont localisées car seule une
région centrale est supercritique grâce à la courbure. Toujours
à cause de la courbure plus forte, le vecteur d'onde critique est
celui où le nombre d'onde orthoradial est nul (si la courbure est
assez forte). Nous avons ainsi au seuil des cibles pulsantes
localisées. Lorsque  est augmenté, la zone supercritique
s'étend et le vecteur d'onde critique de la couronne extérieure de
la zone fraichement instable n'est plus purement radial ! Il ne reste
plus qu'à imaginer quelques effets non-linéaires du type accrochage
pour expliquer que le vecteur d'onde au centre ne soit plus le vecteur
d'onde critique purement radial, mais le même vecteur d'onde que dans
la couronne extérieure de la zone instable. Notons que le comportement
critique de la composante orthoradiale
est augmenté, la zone supercritique
s'étend et le vecteur d'onde critique de la couronne extérieure de
la zone fraichement instable n'est plus purement radial ! Il ne reste
plus qu'à imaginer quelques effets non-linéaires du type accrochage
pour expliquer que le vecteur d'onde au centre ne soit plus le vecteur
d'onde critique purement radial, mais le même vecteur d'onde que dans
la couronne extérieure de la zone instable. Notons que le comportement
critique de la composante orthoradiale 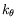 du vecteur d'onde
-- variation linéaire avec
du vecteur d'onde
-- variation linéaire avec  , cf figure
, cf figure ![[*]](crossref.png) --
n'est pas retrouvé par cette interprétation de l'analyse de
stabilité linéaire.
--
n'est pas retrouvé par cette interprétation de l'analyse de
stabilité linéaire.
Toujours à la lumière des résultats du premier chapitre, nous
remarquons que les structures obtenues pour
 peuvent être
purement azimuthales (fleurs à grande hauteur et rayons à petite et
grande hauteur). L'analyse de stabilité linéaire prévoit
effectivement une diminution de la composante radiale dans le cas
peuvent être
purement azimuthales (fleurs à grande hauteur et rayons à petite et
grande hauteur). L'analyse de stabilité linéaire prévoit
effectivement une diminution de la composante radiale dans le cas
 ; néanmoins, l'annulation n'était pas prédite...
; néanmoins, l'annulation n'était pas prédite...




suivant: 5.4.3 Rapports d'aspect et
monter: 5.4 Interprétations en termes
précédent: 5.4.1 Spirales d'Archimède
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ,
nous pouvons non seulement discerner qualitativement entre OH1 et OH2,
mais aussi quantifier l'angle de propagation
,
nous pouvons non seulement discerner qualitativement entre OH1 et OH2,
mais aussi quantifier l'angle de propagation ![[*]](crossref.png) , proposer le petit scénario suivant
pour l'évolution avec
, proposer le petit scénario suivant
pour l'évolution avec ![]() de la structure spatiale des OH2 :
de la structure spatiale des OH2 :
![[*]](crossref.png) --
n'est pas retrouvé par cette interprétation de l'analyse de
stabilité linéaire.
--
n'est pas retrouvé par cette interprétation de l'analyse de
stabilité linéaire.
![]() peuvent être
purement azimuthales (fleurs à grande hauteur et rayons à petite et
grande hauteur). L'analyse de stabilité linéaire prévoit
effectivement une diminution de la composante radiale dans le cas
peuvent être
purement azimuthales (fleurs à grande hauteur et rayons à petite et
grande hauteur). L'analyse de stabilité linéaire prévoit
effectivement une diminution de la composante radiale dans le cas
![]() ; néanmoins, l'annulation n'était pas prédite...
; néanmoins, l'annulation n'était pas prédite...