



suivant: 5.3.3 Fleurs
monter: 5.3 Comportements critiques
précédent: 5.3.1 OH1
Table des matières
5.3.2 OH2
Les ondes hydrothermales de type 2 apparaissent -- tout comme les
OH1 -- via une bifurcation de Hopf supercritique. L'évolution
continue de l'amplitude au seuil est ainsi visible sur la
figure ![[*]](crossref.png) et l'évolution de la fréquence sur la
figure
et l'évolution de la fréquence sur la
figure ![[*]](crossref.png) .
.
Figure:
Evolution de l'amplitude des OH2 pour  mm et
mm et
 .
L'amplitude est mesurée le long de rayons et sa valeur moyennée
dans l'espace
.
L'amplitude est mesurée le long de rayons et sa valeur moyennée
dans l'espace
 est présentée ; il s'agit donc d'une information
globale.
est présentée ; il s'agit donc d'une information
globale.
![\begin{picture}(0,0)(0,0)
\put(220,50){\includegraphics[width=4cm]{raamo2dt}}
\end{picture}](img1124.png) |
Figure:
Evolution de l'amplitude au carré des OH2 pour  mm et
mm et
 .
L'amplitude est mesurée le long d'un cercle et sa valeur moyenne
est présentée, pour des cercles de rayons
.
L'amplitude est mesurée le long d'un cercle et sa valeur moyenne
est présentée, pour des cercles de rayons  mm (
mm (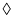 ),
),
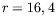 mm (
mm ( ), et
), et 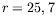 mm (
mm (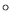 ).
L'amplitude des ondes OH1, mesurée sur un cercle de rayon
).
L'amplitude des ondes OH1, mesurée sur un cercle de rayon 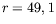 mm
est aussi reportée à titre indicatif.
Les courbes continues représentent des ajustements et guident l'il.
mm
est aussi reportée à titre indicatif.
Les courbes continues représentent des ajustements et guident l'il.
|
|
Figure:
Evolution de la fréquence des OH2 pour  mm et
mm et
 .
.
|
|
La distribution spatiale de ces ondes est -- comme présenté dans la
section précédente -- bien particulière au seuil et son
évolution avec  est originale. L'information spatiale est de
deux types : distribution du vecteur d'onde et position de la structure
dans la cellule. Sur la figure
est originale. L'information spatiale est de
deux types : distribution du vecteur d'onde et position de la structure
dans la cellule. Sur la figure ![[*]](crossref.png) sont visibles les
évolutions avec le paramètre de contrôle des deux composantes
sont visibles les
évolutions avec le paramètre de contrôle des deux composantes
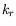 et
et 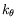 du vecteur d'onde. Alors que la composante
du vecteur d'onde. Alors que la composante 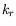 est
finie au seuil et évolue peu avec
est
finie au seuil et évolue peu avec  , la composante azimuthale
, la composante azimuthale
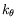 est nulle au seuil -- les ondes sont alors des cibles
pulsantes -- et augmente régulièrement avec
est nulle au seuil -- les ondes sont alors des cibles
pulsantes -- et augmente régulièrement avec  -- les
ondes sont alors des spirales de plus en plus « ouvertes ».
-- les
ondes sont alors des spirales de plus en plus « ouvertes ».
L'évolution de 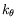 avec le paramètre de contrôle est très
bien ajustée par une loi linéaire. L'extrapolation de cette loi
linéaire au point
avec le paramètre de contrôle est très
bien ajustée par une loi linéaire. L'extrapolation de cette loi
linéaire au point
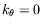 nous redonne approximativement la
valeur du seuil, bien que la mesure soit moins précise que celle de
l'amplitude. Nous avons ainsi la possibilité de définir un second
paramètre d'ordre variant continûment au seuil et avec l'exposant
nous redonne approximativement la
valeur du seuil, bien que la mesure soit moins précise que celle de
l'amplitude. Nous avons ainsi la possibilité de définir un second
paramètre d'ordre variant continûment au seuil et avec l'exposant
 dans la région supercritique. Nous n'avons pas d'interprétation
précise de ce nouveau paramètre d'ordre ; toute explication ne doit
pas négliger la bidimensionnalité non seulement des OH2, mais aussi
de la géométrie de la cellule.
dans la région supercritique. Nous n'avons pas d'interprétation
précise de ce nouveau paramètre d'ordre ; toute explication ne doit
pas négliger la bidimensionnalité non seulement des OH2, mais aussi
de la géométrie de la cellule.
Figure:
Evolution du vecteur d'onde des OH2 pour  mm et
mm et
 .
A gauche :
.
A gauche : 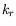 ; à droite :
; à droite : 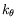 .
.
|
|
La structure des OH2 est localisée près du plot central. La
figure ![[*]](crossref.png) présente une succession de profils
radiaux d'amplitude : nous y voyons l'instabilité s'étendre lorsque
présente une succession de profils
radiaux d'amplitude : nous y voyons l'instabilité s'étendre lorsque
 est augmenté. Nous avons quantifié l'envahissement
progressif de la cellule par les OH2. Comme dans le cas des rouleaux
corotatifs de l'écoulement de base, nous avons mesuré la position du
front des OH2 dans la cellule en définissant cette position comme le
rayon du point dont l'amplitude est la moitié de l'amplitude maximale.
Cette grandeur est reportée sur la figure
est augmenté. Nous avons quantifié l'envahissement
progressif de la cellule par les OH2. Comme dans le cas des rouleaux
corotatifs de l'écoulement de base, nous avons mesuré la position du
front des OH2 dans la cellule en définissant cette position comme le
rayon du point dont l'amplitude est la moitié de l'amplitude maximale.
Cette grandeur est reportée sur la figure ![[*]](crossref.png) . Nous
observons un comportement régulier, linéaire en
. Nous
observons un comportement régulier, linéaire en  de la
position du front des OH2 dans la cellule.
de la
position du front des OH2 dans la cellule.
Figure:
Empilement de profils radiaux d'amplitude locale pour  mm et
différents
mm et
différents
 : 8, 9, 10, 11, 12, 14, 16, 18 et 20 K.
Pour des raisons de clarté, les profils ont été décalés
dans la direction verticale d'un facteur proportionnel à
: 8, 9, 10, 11, 12, 14, 16, 18 et 20 K.
Pour des raisons de clarté, les profils ont été décalés
dans la direction verticale d'un facteur proportionnel à  .
Sur le dernier profil (
.
Sur le dernier profil (
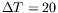 K), les OH1 sont présentes
et l'amplitude est finie partout dans la cellule.
K), les OH1 sont présentes
et l'amplitude est finie partout dans la cellule.
|
|
Figure:
Evolution de la position du front des OH2 pour  mm et
mm et
 .
.
|
|
Un élargissement du pic correspondant aux OH2 dans les spectres est
observé lorsque la différence de température est augmentée
(figure ![[*]](crossref.png) ). Nous mesurons alors la largeur du
pic à mi-hauteur et la reportons sur la
figure
). Nous mesurons alors la largeur du
pic à mi-hauteur et la reportons sur la
figure ![[*]](crossref.png) . Cette grandeur est une mesure de
l'élargissement de la bande de modes instables. De plus, si la hauteur
du pic principal est fixée -- ce qui semble à peu près le
cas --, sa largeur est proportionnelle à l'aire sous le pic, qui
mesure l'énergie contenue dans l'ensemble des modes instables. Le
théorème de Parseval relie alors cette énergie à l'énergie
moyenne mesurée dans l'espace direct, i.e., la moyenne spatiale du
carré de l'amplitude de l'onde après filtrage. Nous observons le
même comportement que sur la figure
. Cette grandeur est une mesure de
l'élargissement de la bande de modes instables. De plus, si la hauteur
du pic principal est fixée -- ce qui semble à peu près le
cas --, sa largeur est proportionnelle à l'aire sous le pic, qui
mesure l'énergie contenue dans l'ensemble des modes instables. Le
théorème de Parseval relie alors cette énergie à l'énergie
moyenne mesurée dans l'espace direct, i.e., la moyenne spatiale du
carré de l'amplitude de l'onde après filtrage. Nous observons le
même comportement que sur la figure ![[*]](crossref.png) qui
représente le carré de l'amplitude moyenne. La largeur du pic
principal correspondant aux OH2 se comporte comme un paramètre d'ordre
avec la puissance 1/2.
qui
représente le carré de l'amplitude moyenne. La largeur du pic
principal correspondant aux OH2 se comporte comme un paramètre d'ordre
avec la puissance 1/2.
Figure:
Empilement de spectres réalisés pour  mm et différents
mm et différents
 : 8, 10, 12, 16 et 20 K. L'élargissement du pic correspondant
aux OH2 est visible alors que sa hauteur par rapport au niveau de bruit est à
peu près constante.
: 8, 10, 12, 16 et 20 K. L'élargissement du pic correspondant
aux OH2 est visible alors que sa hauteur par rapport au niveau de bruit est à
peu près constante.
|
|
Figure:
Evolution de la largeur du pic des OH2 dans le spectre temporel
pour  mm et
mm et
 ; une moyenne est effectuée
selon la direction radiale. Un comportement critique se dégage nettement.
; une moyenne est effectuée
selon la direction radiale. Un comportement critique se dégage nettement.
![\begin{picture}(0,0)(0,0)
\put(220,50){\includegraphics[width=4cm]{dfreq2dt}}
\end{picture}](img1139.png) |




suivant: 5.3.3 Fleurs
monter: 5.3 Comportements critiques
précédent: 5.3.1 OH1
Table des matières
Nicolas Garnier - Thèse de doctorat
![\includegraphics[width=8cm]{raamo-dt}](img1123.png)
![\begin{picture}(0,0)(0,0)
\put(220,50){\includegraphics[width=4cm]{raamo2dt}}
\end{picture}](img1124.png)
![[*]](crossref.png) et l'évolution de la fréquence sur la
figure
et l'évolution de la fréquence sur la
figure ![[*]](crossref.png) .
.
![\includegraphics[width=8cm]{raamo-dt}](img1123.png)
![\begin{picture}(0,0)(0,0)
\put(220,50){\includegraphics[width=4cm]{raamo2dt}}
\end{picture}](img1124.png)
![\includegraphics[width=12cm]{calla2dt}](img1125.png)
![]() est originale. L'information spatiale est de
deux types : distribution du vecteur d'onde et position de la structure
dans la cellule. Sur la figure
est originale. L'information spatiale est de
deux types : distribution du vecteur d'onde et position de la structure
dans la cellule. Sur la figure ![[*]](crossref.png) sont visibles les
évolutions avec le paramètre de contrôle des deux composantes
sont visibles les
évolutions avec le paramètre de contrôle des deux composantes
![]() et
et ![]() du vecteur d'onde. Alors que la composante
du vecteur d'onde. Alors que la composante ![]() est
finie au seuil et évolue peu avec
est
finie au seuil et évolue peu avec ![]() , la composante azimuthale
, la composante azimuthale
![]() est nulle au seuil -- les ondes sont alors des cibles
pulsantes -- et augmente régulièrement avec
est nulle au seuil -- les ondes sont alors des cibles
pulsantes -- et augmente régulièrement avec ![]() -- les
ondes sont alors des spirales de plus en plus « ouvertes ».
-- les
ondes sont alors des spirales de plus en plus « ouvertes ».
![]() avec le paramètre de contrôle est très
bien ajustée par une loi linéaire. L'extrapolation de cette loi
linéaire au point
avec le paramètre de contrôle est très
bien ajustée par une loi linéaire. L'extrapolation de cette loi
linéaire au point
![]() nous redonne approximativement la
valeur du seuil, bien que la mesure soit moins précise que celle de
l'amplitude. Nous avons ainsi la possibilité de définir un second
paramètre d'ordre variant continûment au seuil et avec l'exposant
nous redonne approximativement la
valeur du seuil, bien que la mesure soit moins précise que celle de
l'amplitude. Nous avons ainsi la possibilité de définir un second
paramètre d'ordre variant continûment au seuil et avec l'exposant
![]() dans la région supercritique. Nous n'avons pas d'interprétation
précise de ce nouveau paramètre d'ordre ; toute explication ne doit
pas négliger la bidimensionnalité non seulement des OH2, mais aussi
de la géométrie de la cellule.
dans la région supercritique. Nous n'avons pas d'interprétation
précise de ce nouveau paramètre d'ordre ; toute explication ne doit
pas négliger la bidimensionnalité non seulement des OH2, mais aussi
de la géométrie de la cellule.
![[*]](crossref.png) présente une succession de profils
radiaux d'amplitude : nous y voyons l'instabilité s'étendre lorsque
présente une succession de profils
radiaux d'amplitude : nous y voyons l'instabilité s'étendre lorsque
![]() est augmenté. Nous avons quantifié l'envahissement
progressif de la cellule par les OH2. Comme dans le cas des rouleaux
corotatifs de l'écoulement de base, nous avons mesuré la position du
front des OH2 dans la cellule en définissant cette position comme le
rayon du point dont l'amplitude est la moitié de l'amplitude maximale.
Cette grandeur est reportée sur la figure
est augmenté. Nous avons quantifié l'envahissement
progressif de la cellule par les OH2. Comme dans le cas des rouleaux
corotatifs de l'écoulement de base, nous avons mesuré la position du
front des OH2 dans la cellule en définissant cette position comme le
rayon du point dont l'amplitude est la moitié de l'amplitude maximale.
Cette grandeur est reportée sur la figure ![[*]](crossref.png) . Nous
observons un comportement régulier, linéaire en
. Nous
observons un comportement régulier, linéaire en ![]() de la
position du front des OH2 dans la cellule.
de la
position du front des OH2 dans la cellule.
![\includegraphics[width=8cm]{prf-6-dt}](img1135.png)
![[*]](crossref.png) ). Nous mesurons alors la largeur du
pic à mi-hauteur et la reportons sur la
figure
). Nous mesurons alors la largeur du
pic à mi-hauteur et la reportons sur la
figure ![[*]](crossref.png) . Cette grandeur est une mesure de
l'élargissement de la bande de modes instables. De plus, si la hauteur
du pic principal est fixée -- ce qui semble à peu près le
cas --, sa largeur est proportionnelle à l'aire sous le pic, qui
mesure l'énergie contenue dans l'ensemble des modes instables. Le
théorème de Parseval relie alors cette énergie à l'énergie
moyenne mesurée dans l'espace direct, i.e., la moyenne spatiale du
carré de l'amplitude de l'onde après filtrage. Nous observons le
même comportement que sur la figure
. Cette grandeur est une mesure de
l'élargissement de la bande de modes instables. De plus, si la hauteur
du pic principal est fixée -- ce qui semble à peu près le
cas --, sa largeur est proportionnelle à l'aire sous le pic, qui
mesure l'énergie contenue dans l'ensemble des modes instables. Le
théorème de Parseval relie alors cette énergie à l'énergie
moyenne mesurée dans l'espace direct, i.e., la moyenne spatiale du
carré de l'amplitude de l'onde après filtrage. Nous observons le
même comportement que sur la figure ![[*]](crossref.png) qui
représente le carré de l'amplitude moyenne. La largeur du pic
principal correspondant aux OH2 se comporte comme un paramètre d'ordre
avec la puissance 1/2.
qui
représente le carré de l'amplitude moyenne. La largeur du pic
principal correspondant aux OH2 se comporte comme un paramètre d'ordre
avec la puissance 1/2.
![\includegraphics[width=8cm]{spec6-dt}](img1137.png)
![\includegraphics[width=8cm]{dfreq-dt}](img1138.png)
![\begin{picture}(0,0)(0,0)
\put(220,50){\includegraphics[width=4cm]{dfreq2dt}}
\end{picture}](img1139.png)