



suivant: B.3.0.2 Limite convectif/absolu
monter: B.3 Prédictions
précédent: B.3 Prédictions
Table des matières
Nous pouvons chercher analytiquement la limite de stabilité d'une
solution de Stokes de l'équation
 GL modifiée, dans la limite des
perturbations de grande longueur d'onde
GL modifiée, dans la limite des
perturbations de grande longueur d'onde
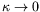 . Pour
cela, nous recherchons le coefficient de diffusion de la phase :
. Pour
cela, nous recherchons le coefficient de diffusion de la phase :
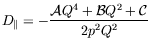 |
(B.2) |
où
Nous trouvons alors que pour chaque valeur de  , deux racines
sont possibles car
, deux racines
sont possibles car
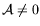 si les nouveaux termes ne s'annulent
pas. Cela signifie qu'outre la courbe de stabilité d'Eckhaus
« classique » tangente localement à la courbe de stabilité
marginale, il existe une seconde courbe qui peut refermer le ballon pour
des valeurs finies de
si les nouveaux termes ne s'annulent
pas. Cela signifie qu'outre la courbe de stabilité d'Eckhaus
« classique » tangente localement à la courbe de stabilité
marginale, il existe une seconde courbe qui peut refermer le ballon pour
des valeurs finies de  .
.
Les figures ![[*]](crossref.png) et
et ![[*]](crossref.png) présentent les courbes obtenues sur des cas réalistes : les
coefficients sont ceux mesurés lors des expériences (cf
annexe
présentent les courbes obtenues sur des cas réalistes : les
coefficients sont ceux mesurés lors des expériences (cf
annexe ![[*]](crossref.png) ). Nous proposons néanmoins des valeurs
différentes des coefficients du terme 1 (non déterminés
expérimentalement) afin d'illustrer la grande richesse de
l'équation.
). Nous proposons néanmoins des valeurs
différentes des coefficients du terme 1 (non déterminés
expérimentalement) afin d'illustrer la grande richesse de
l'équation.
L'information donnée dans la limite
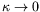 par
l'expression analytique de
par
l'expression analytique de
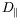 nous donne la limite de
l'instabilité d'Eckhaus que nous définissons comme l'instabilité
modulationnelle à très grande longueur d'onde. Nous avons
complété cette information en recherchant numériquement la limite
d'instabilité modulationnelle à nombre d'onde
nous donne la limite de
l'instabilité d'Eckhaus que nous définissons comme l'instabilité
modulationnelle à très grande longueur d'onde. Nous avons
complété cette information en recherchant numériquement la limite
d'instabilité modulationnelle à nombre d'onde 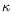 quelconque.
Nous avons ainsi vérifié que la limite d'Eckhaus représentée par
la parabole tangente en
quelconque.
Nous avons ainsi vérifié que la limite d'Eckhaus représentée par
la parabole tangente en
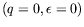 à la courbe de stabilité
marginale était la seule limite possible. Cela signifie entre autres
qu'une diminution de
à la courbe de stabilité
marginale était la seule limite possible. Cela signifie entre autres
qu'une diminution de  conduit toujours à l'instabilité
d'Eckhaus, i.e. à grande longueur d'onde.
conduit toujours à l'instabilité
d'Eckhaus, i.e. à grande longueur d'onde.
Au contraire, nous avons constaté que la courbe d'Eckhaus « du
dessus » (à valeur finie de  pour
pour 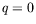 ) n'est pas toujours
la plus dangereuse et qu'une instabilité à petite longueur d'onde
peut survenir par augmentation de
) n'est pas toujours
la plus dangereuse et qu'une instabilité à petite longueur d'onde
peut survenir par augmentation de  . Cette instabilité est
peut-être liée au choix du terme 3 (
. Cette instabilité est
peut-être liée au choix du terme 3 (
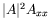 ) qui est instable
vis-à-vis des gradients de phase.
) qui est instable
vis-à-vis des gradients de phase.




suivant: B.3.0.2 Limite convectif/absolu
monter: B.3 Prédictions
précédent: B.3 Prédictions
Table des matières
Nicolas Garnier - Thèse de doctorat
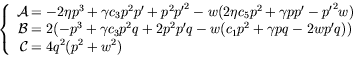
![[*]](crossref.png) et
et ![[*]](crossref.png) présentent les courbes obtenues sur des cas réalistes : les
coefficients sont ceux mesurés lors des expériences (cf
annexe
présentent les courbes obtenues sur des cas réalistes : les
coefficients sont ceux mesurés lors des expériences (cf
annexe ![[*]](crossref.png) ). Nous proposons néanmoins des valeurs
différentes des coefficients du terme 1 (non déterminés
expérimentalement) afin d'illustrer la grande richesse de
l'équation.
). Nous proposons néanmoins des valeurs
différentes des coefficients du terme 1 (non déterminés
expérimentalement) afin d'illustrer la grande richesse de
l'équation.
![]() par
l'expression analytique de
par
l'expression analytique de
![]() nous donne la limite de
l'instabilité d'Eckhaus que nous définissons comme l'instabilité
modulationnelle à très grande longueur d'onde. Nous avons
complété cette information en recherchant numériquement la limite
d'instabilité modulationnelle à nombre d'onde
nous donne la limite de
l'instabilité d'Eckhaus que nous définissons comme l'instabilité
modulationnelle à très grande longueur d'onde. Nous avons
complété cette information en recherchant numériquement la limite
d'instabilité modulationnelle à nombre d'onde ![]() quelconque.
Nous avons ainsi vérifié que la limite d'Eckhaus représentée par
la parabole tangente en
quelconque.
Nous avons ainsi vérifié que la limite d'Eckhaus représentée par
la parabole tangente en
![]() à la courbe de stabilité
marginale était la seule limite possible. Cela signifie entre autres
qu'une diminution de
à la courbe de stabilité
marginale était la seule limite possible. Cela signifie entre autres
qu'une diminution de ![]() conduit toujours à l'instabilité
d'Eckhaus, i.e. à grande longueur d'onde.
conduit toujours à l'instabilité
d'Eckhaus, i.e. à grande longueur d'onde.