



suivant: B.3.0.3 Conclusions
monter: B.3 Prédictions
précédent: B.3.0.1 Courbe d'Eckhaus
Table des matières
Seule la limite de stabilité convective d'Eckhaus est donnée par le
calcul précédent. Dans le cas d'une cellule de taille finie, la
limite absolue est la plus intéressante, mais les calculs sont
beaucoup plus délicats. En effet, il n'est plus possible de prendre
seulement la limite
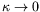 , car la partie imaginaire du
nombre d'onde intervient aussi ; le calcul doit être effectué dans
le plan complexe.
, car la partie imaginaire du
nombre d'onde intervient aussi ; le calcul doit être effectué dans
le plan complexe.
Nous avons rédigé un programme permettant, en cherchant le point
selle de la surface du taux de croissance temporel dans le plan
complexe, d'approcher la limite convectif/absolu de l'instabilité
modulationnelle. Nous ne nous restreignons alors pas à la limite des
perturbations de grande longueur d'onde. Les courbes limites obtenues
sont reproduites sur chaque figure à côté des courbes limites
« convectives ». La figure ![[*]](crossref.png) illustre les
différentes régions obtenues dans le cas d'une équation de
Ginzburg-Landau non modifiée.
illustre les
différentes régions obtenues dans le cas d'une équation de
Ginzburg-Landau non modifiée.
Figure:
Courbes de stabilité marginale et de stabilité d'Eckhaus
pour l'équation de Ginzburg-Landau habituelle avec
{ =0,
=0, 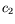 =1}.
Le graphe de gauche présente la parabole de stabilité marginale
et la parabole d'Eckhaus (ES : états stables vis-à-vis d'Eckhaus,
AI : états instables vis-à-vis d'Eckhaus). Le graphe de droite
présente les différentes régions dans le cas d'une boîte
non périodique. OCI et OAI représentent les régions où l'instabilité
primaire en ondes est respectivement convective et absolue ; ces régions
sont séparées par une droite horizontale d'équation
=1}.
Le graphe de gauche présente la parabole de stabilité marginale
et la parabole d'Eckhaus (ES : états stables vis-à-vis d'Eckhaus,
AI : états instables vis-à-vis d'Eckhaus). Le graphe de droite
présente les différentes régions dans le cas d'une boîte
non périodique. OCI et OAI représentent les régions où l'instabilité
primaire en ondes est respectivement convective et absolue ; ces régions
sont séparées par une droite horizontale d'équation
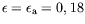 (cf chapitre
(cf chapitre ![[*]](crossref.png) ).
La vitesse de groupe adimensionnée est prise égale à
).
La vitesse de groupe adimensionnée est prise égale à
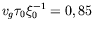 , conformément aux mesures expérimentales.
ES, ECI et EAI repèrent les zones stable, convectivement instable
et absolument instable d'Eckhaus. La croix (
, conformément aux mesures expérimentales.
ES, ECI et EAI repèrent les zones stable, convectivement instable
et absolument instable d'Eckhaus. La croix (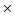 ) note l'absence de
solution en dehors de la parabole de stabilité marginale.
) note l'absence de
solution en dehors de la parabole de stabilité marginale.
![\begin{picture}(0,0)(0,0)
\put(132,250){\makebox(0,0)[b]{anneau (c.l. p\'eriodi...
...put(362,250){\makebox(0,0)[b]{rectangle (c.l. non p\'eriodiques)}}
\end{picture}](img1240.png) |
Figure:
Courbes de stabilité marginale et de stabilité d'Eckhaus
pour { =0,
=0, 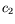 =1,
=1, 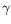 =-0.4,
=-0.4, 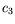 =0,
=0, 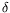 =-0.6,
=-0.6,
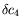 =0.58,
=0.58, 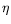 =-1.7,
=-1.7, 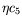 =0.5}.
La figure de gauche présente les limites d'Eckhaus convectif
déduite de la formule
=0.5}.
La figure de gauche présente les limites d'Eckhaus convectif
déduite de la formule ![[*]](crossref.png) (
(
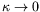 )
(trait plein)
ainsi que la limite vis-à-vis de perturbations de nombre d'onde
)
(trait plein)
ainsi que la limite vis-à-vis de perturbations de nombre d'onde
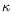 quelconque (trait pointillé).
Les différentes régions sont notées
ES, EI : stable, instable vis-à-vis des modulations de petit nombre d'onde.
SWI : instable vis-à-vis des modulations de nombre d'onde non nul.
La figure de droite présente en plus la limite convectif/absolu
d'Eckhaus, qui donne dans le rectangle une zone d'observation des états homogènes
plus étendue. La vitesse de groupe adimensionnée est pour
ce dernier cas choisie égale à 0,85. La droite horizontale
correspond à
quelconque (trait pointillé).
Les différentes régions sont notées
ES, EI : stable, instable vis-à-vis des modulations de petit nombre d'onde.
SWI : instable vis-à-vis des modulations de nombre d'onde non nul.
La figure de droite présente en plus la limite convectif/absolu
d'Eckhaus, qui donne dans le rectangle une zone d'observation des états homogènes
plus étendue. La vitesse de groupe adimensionnée est pour
ce dernier cas choisie égale à 0,85. La droite horizontale
correspond à
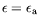 , i.e. à le limite
convectif/absolu pour l'instabilité primaire en ondes.
ECI, EAI : Eckhaus convectivement et absolument instable.
Noter que la courbe en pointillés limitant par le haut la région
convectivement instable a été calculée vis-à-vis de perturbations
de nombre d'onde
, i.e. à le limite
convectif/absolu pour l'instabilité primaire en ondes.
ECI, EAI : Eckhaus convectivement et absolument instable.
Noter que la courbe en pointillés limitant par le haut la région
convectivement instable a été calculée vis-à-vis de perturbations
de nombre d'onde 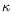 quelconque, non nécessairement petit.
quelconque, non nécessairement petit.
![\begin{picture}(0,0)(0,0)
\put(132,250){\makebox(0,0)[b]{anneau (c.l. p\'eriodi...
...put(362,250){\makebox(0,0)[b]{rectangle (c.l. non p\'eriodiques)}}
\end{picture}](img1240.png) |
Figure:
Courbes de stabilité marginale et de stabilité d'Eckhaus
pour { =0,
=0, 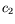 =1,
=1, 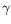 =+0.4,
=+0.4, 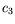 =0,
=0, 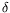 =-0.6,
=-0.6,
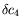 =0.58,
=0.58, 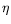 =-1.7,
=-1.7, 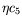 =0.5La figure de gauche présente les limites d'Eckhaus convectif
déduite de la formule
=0.5La figure de gauche présente les limites d'Eckhaus convectif
déduite de la formule ![[*]](crossref.png) (
(
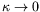 )
(trait plein)
ainsi que la limite vis-à-vis de perturbations de nombre d'onde
)
(trait plein)
ainsi que la limite vis-à-vis de perturbations de nombre d'onde
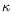 quelconque (courbe centrale).
Les différentes régions sont notées
ES, EI : stable, instable vis-à-vis des modulations de petit nombre d'onde.
SWI : instable vis-à-vis des modulations de nombre d'onde non nul.
La figure de droite présente en plus la limite convectif/absolu
d'Eckhaus. La vitesse de groupe adimensionnée est pour
ce dernier cas choisie égale à 0,85. La droite horizontale
correspond à
quelconque (courbe centrale).
Les différentes régions sont notées
ES, EI : stable, instable vis-à-vis des modulations de petit nombre d'onde.
SWI : instable vis-à-vis des modulations de nombre d'onde non nul.
La figure de droite présente en plus la limite convectif/absolu
d'Eckhaus. La vitesse de groupe adimensionnée est pour
ce dernier cas choisie égale à 0,85. La droite horizontale
correspond à
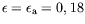 , i.e. à la limite
convectif/absolu pour l'instabilité primaire en ondes.
ECI, EAI : Eckhaus convectivement et absolument instable.
Noter qu'à la verticale de
, i.e. à la limite
convectif/absolu pour l'instabilité primaire en ondes.
ECI, EAI : Eckhaus convectivement et absolument instable.
Noter qu'à la verticale de 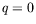 une fine bande d'instabilité d'Eckhaus
convective existe ; sa largeur en terme de
une fine bande d'instabilité d'Eckhaus
convective existe ; sa largeur en terme de  est de l'ordre
de 0,1 K tout comme observé expérimentalement
(§
est de l'ordre
de 0,1 K tout comme observé expérimentalement
(§ ![[*]](crossref.png) ).
).
![\begin{picture}(0,0)(0,0)
\put(132,250){\makebox(0,0)[b]{anneau (c.l. p\'eriodi...
...put(362,250){\makebox(0,0)[b]{rectangle (c.l. non p\'eriodiques)}}
\end{picture}](img1240.png) |




suivant: B.3.0.3 Conclusions
monter: B.3 Prédictions
précédent: B.3.0.1 Courbe d'Eckhaus
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) illustre les
différentes régions obtenues dans le cas d'une équation de
Ginzburg-Landau non modifiée.
illustre les
différentes régions obtenues dans le cas d'une équation de
Ginzburg-Landau non modifiée.
![\includegraphics[width=8cm]{Eck-c-00}](img1238.png)
![\includegraphics[width=8cm]{Eck-a-00}](img1239.png)
![\includegraphics[width=8cm]{Eck-c-04}](img1243.png)
![\includegraphics[width=8cm]{Eck-a-04}](img1244.png)
![\includegraphics[width=8cm]{Eck-c-05}](img1250.png)
![\includegraphics[width=8cm]{Eck-a-05}](img1251.png)