



suivant: C. Déterminations expérimentales des
monter: B.3 Prédictions
précédent: B.3.0.2 Limite convectif/absolu
Table des matières
Les différentes courbes obtenues sont commentées dans les légendes
des figures. Nous pouvons remarquer qu'une légère modification d'un
des paramètres (le changement du signe de 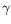 entre les
figures
entre les
figures ![[*]](crossref.png) et
et ![[*]](crossref.png) par exemple)
altère grandement l'aspect qualitatif du ballon de stabilité.
par exemple)
altère grandement l'aspect qualitatif du ballon de stabilité.
Nous observons ainsi que pour certaines gammes de paramètres, le
ballon calculé à l'aide de
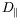 dans la limite
dans la limite
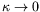 peut être constitué de deux régions distinctes. Une
telle situation semble correspondre aux observations expérimentales
qui révèlent l'existence d'une zone de « turbulence » autour de
peut être constitué de deux régions distinctes. Une
telle situation semble correspondre aux observations expérimentales
qui révèlent l'existence d'une zone de « turbulence » autour de
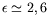 pour laquelle aucun nombre d'onde
pour laquelle aucun nombre d'onde 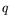 n'est
stable. Tempérons néanmoins notre enthousiasme en remarquant que
l'analyse numérique des perturbations de nombre d'onde
n'est
stable. Tempérons néanmoins notre enthousiasme en remarquant que
l'analyse numérique des perturbations de nombre d'onde 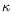 quelconque exclut la seconde région de stabilité située plus
haut en
quelconque exclut la seconde région de stabilité située plus
haut en  . Cette configuration est celle de la
figure
. Cette configuration est celle de la
figure ![[*]](crossref.png) . Notre optimisme ne doit toutefois pas
disparaître si nous rappellons que le terme 3 utilisé pour
modifier l'équation d'amplitude lui confère une instabilité
vis-à-vis des gradients de phase ; cette instabilité conjecturelle
disparaît sans doute en considérant un autre terme d'ordre 5
comme
. Notre optimisme ne doit toutefois pas
disparaître si nous rappellons que le terme 3 utilisé pour
modifier l'équation d'amplitude lui confère une instabilité
vis-à-vis des gradients de phase ; cette instabilité conjecturelle
disparaît sans doute en considérant un autre terme d'ordre 5
comme 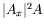 : une telle étude est en cours.
: une telle étude est en cours.
Il est en fait possible d'obtenir analytiquement une asymptote de la
courbe limitant l'instabilité à grand nombre d'onde. En prenant la
limite
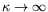 , nous trouvons l'équation :
, nous trouvons l'équation :
où apparaît clairement le rôle du coefficient 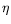 du terme 3. La limite
du terme 3. La limite
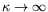 est toutefois à
prendre avec précaution et nous nous garderons de toute autre
conclusion à ce sujet.
est toutefois à
prendre avec précaution et nous nous garderons de toute autre
conclusion à ce sujet.
Nos calculs révèlent aussi l'extraordinaire complexification liée
à la prise en compte de la distinction convectif/absolu. Les
diagrammes de stabilité n'ont ainsi pas la même allure dans l'anneau
-- où le nombre d'onde est discret et peut prendre une valeur
différente de sa valeur au seuil -- et dans le rectangle -- où
seul un nombre d'onde est sélectionné pour les plus faibles valeurs
de  .
.
Enfin, une fois notée la grande sensibilité qualitative du ballon
vis-à-vis des valeurs des coefficients, il est important de préciser
que les mesures expérimentales de ces derniers sont délicates et
n'offre pas (encore ?) la précision nécessaire à toute conclusion
définitive. L'annexe suivante est consacrée à ces mesures.




suivant: C. Déterminations expérimentales des
monter: B.3 Prédictions
précédent: B.3.0.2 Limite convectif/absolu
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) . Notre optimisme ne doit toutefois pas
disparaître si nous rappellons que le terme 3 utilisé pour
modifier l'équation d'amplitude lui confère une instabilité
vis-à-vis des gradients de phase ; cette instabilité conjecturelle
disparaît sans doute en considérant un autre terme d'ordre 5
comme
. Notre optimisme ne doit toutefois pas
disparaître si nous rappellons que le terme 3 utilisé pour
modifier l'équation d'amplitude lui confère une instabilité
vis-à-vis des gradients de phase ; cette instabilité conjecturelle
disparaît sans doute en considérant un autre terme d'ordre 5
comme