



suivant: 3.2.2 Cas de l'expérience
monter: 3.2 Instabilité secondaire des
précédent: 3.2 Instabilité secondaire des
Table des matières
Les calculs de stabilité linéaire d'une solution de Stokes non nulle
vis-à-vis de perturbations d'amplitude et de phase ont été
réalisés par Fauve (1987), Matkowsky et Volpert (1993) pour l'instabilité
convective en géométrie infinie. Tuckerman et Barkley (1990) ont étudié
l'effet de la discrétisation dans le cas des conditions aux limites
périodiques; ils ont ainsi mis en évidence un décalage de la
région de stabilité (parabole d'Eckhaus, définie en
annexe ![[*]](crossref.png) ) vers les plus petites valeurs du paramètre
de contrôle. Ce décalage -- de
) vers les plus petites valeurs du paramètre
de contrôle. Ce décalage -- de
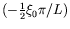 pour
l'équation de Ginzburg-Landau réelle -- permet au nombre d'onde
discret le plus critique d'être stable vis-à-vis des modulations
d'Eckhaus lorsqu'il apparaît. La prise en compte de la transition
entre instabilité convective et absolue est plus ardue.
Huerre (1988) a abordé la question analytiquement dans le cas de
IRGL. Dans le cas de
pour
l'équation de Ginzburg-Landau réelle -- permet au nombre d'onde
discret le plus critique d'être stable vis-à-vis des modulations
d'Eckhaus lorsqu'il apparaît. La prise en compte de la transition
entre instabilité convective et absolue est plus ardue.
Huerre (1988) a abordé la question analytiquement dans le cas de
IRGL. Dans le cas de
 GL, Deissler (1987) a abordé
qualitativement le problème avec une étude numérique, en observant
le régime convectivement instable d'Eckhaus grâce à une source de
bruit placée à la paroi amont du domaine. Müller et Tveitereid (1995) ont
numériquement isolé les différents domaines de stabilité dans le
plan
GL, Deissler (1987) a abordé
qualitativement le problème avec une étude numérique, en observant
le régime convectivement instable d'Eckhaus grâce à une source de
bruit placée à la paroi amont du domaine. Müller et Tveitereid (1995) ont
numériquement isolé les différents domaines de stabilité dans le
plan
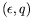 et Couairon et Chomaz (1999) étudié les modes globaux
correspondants ; une présentation complète de ces résultats peut
être trouvée dans l'article de Chomaz et al. (1999).
et Couairon et Chomaz (1999) étudié les modes globaux
correspondants ; une présentation complète de ces résultats peut
être trouvée dans l'article de Chomaz et al. (1999).
Nous ne reproduisons ici que des résultats expérimentaux. Le cas de
l'anneau est brièvement rappellé et commenté. Le cas du rectangle
est décrit en détail ; sa configuration est la même que dans
l'étude du premier seuil : 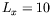 mm et
mm et 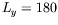 mm.
mm.




suivant: 3.2.2 Cas de l'expérience
monter: 3.2 Instabilité secondaire des
précédent: 3.2 Instabilité secondaire des
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ) vers les plus petites valeurs du paramètre
de contrôle. Ce décalage -- de
) vers les plus petites valeurs du paramètre
de contrôle. Ce décalage -- de
![]() mm et
mm et ![]() mm.
mm.