3.2 Instabilité secondaire des ondes hydrothermales

A une dimension d'espace, comme nous nous y sommes restreints ici, nous savons que les ondes non-linéaires ne peuvent être sujettes -- du point de vue de la phase -- qu'à l'instabilité modulationnelle à petit nombre d'onde ( 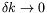$\delta k \rightarrow 0$) dite d'Eckhaus. La vitesse de groupe des ondes hydrothermales restant finie lorsque $\epsilon$ est augmenté et que survient cette instabilité secondaire, nous devons discerner entre la nature convective ou absolue de l'instabilité d'Eckhaus comme nous l'avons fait pour l'instabilité primaire.

Nous évoquons ici encore l'étude du modèle de ${\mathbb{C}}$GL dans le cas d'une onde unique. Nous rappellons ensuite les résultats expérimentaux de Mukolobwiez et al. (1998) qui ont observé l'instabilité d'Eckhaus des ondes hydrothermales dans l'anneau ; l'annexe  rappelle et complète cette étude avant d'en proposer une modélisation originale. Nous décrivons ensuite en détail les observations expérimentales dans la géométrie rectangulaire non périodique où nous illustrons l'instabilité d'Eckhaus absolue et convective.