



suivant: 4.1.3 Hauteur de fluide
monter: 4.1 Profils de température
précédent: 4.1.1 Protocole
Table des matières
4.1.2 Hauteur de fluide  =1.9 mm
=1.9 mm
La figure ![[*]](crossref.png) représente les différents profils
radiaux mesurés pour
représente les différents profils
radiaux mesurés pour
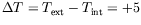 K, ainsi que leur moyenne représentant le profil moyen après
intégration suivant
K, ainsi que leur moyenne représentant le profil moyen après
intégration suivant 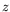 . Ces profils présentent une oscillation
spatiale d'amplitude
. Ces profils présentent une oscillation
spatiale d'amplitude 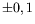 K, qui est en fait la signature des
oscillations temporelles des températures
K, qui est en fait la signature des
oscillations temporelles des températures
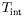 et
et
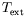 autour de leur valeur de consigne. Ces oscillations
peuvent être fortement amorties si l'on règle soigneusement les
paramètres de régulation des bains thermostatés ; cette opération
est à renouveller à chaque changement des températures de consigne
et surtout lors d'une inversion de
autour de leur valeur de consigne. Ces oscillations
peuvent être fortement amorties si l'on règle soigneusement les
paramètres de régulation des bains thermostatés ; cette opération
est à renouveller à chaque changement des températures de consigne
et surtout lors d'une inversion de  , ce que nous avons souvent
omis. La longueur d'onde de ces oscillations spatiales est
proportionelle à la vitesse de déplacement du thermocouple dans la
cellule ; nous vérifions ainsi que la période des oscillations
thermiques parasites est de l'ordre de 2 minutes. Ces oscillations
disparaissent lorsque l'on moyenne plusieurs profils, ou que l'on balaye
la cellule en intégrant les valeurs en chaque point sur un temps
très long.
, ce que nous avons souvent
omis. La longueur d'onde de ces oscillations spatiales est
proportionelle à la vitesse de déplacement du thermocouple dans la
cellule ; nous vérifions ainsi que la période des oscillations
thermiques parasites est de l'ordre de 2 minutes. Ces oscillations
disparaissent lorsque l'on moyenne plusieurs profils, ou que l'on balaye
la cellule en intégrant les valeurs en chaque point sur un temps
très long.
Figure:
Profils de température expérimentaux radiaux
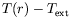 pour 4 mm
pour 4 mm 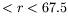 mm (
mm (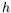 =1,9 mm,
=1,9 mm,  =+5K). A gauche :
les différentes courbes en traits pleins correspondent, de haut en bas,
à
=+5K). A gauche :
les différentes courbes en traits pleins correspondent, de haut en bas,
à 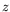 =1.9 mm (à la surface), 1.5, 1.1, 0.7, 0.3 mm.
A droite : profil moyen. Sur chacun des graphes, la courbe
en pointillés représente le profil conductif théorique.
Les oscillations spatiales sont dues à l'oscillation à très
basse fréquence des régulations de température.
=1.9 mm (à la surface), 1.5, 1.1, 0.7, 0.3 mm.
A droite : profil moyen. Sur chacun des graphes, la courbe
en pointillés représente le profil conductif théorique.
Les oscillations spatiales sont dues à l'oscillation à très
basse fréquence des régulations de température.
|
|
La figure ![[*]](crossref.png) présente alors les profils moyens
obtenus pour différents
présente alors les profils moyens
obtenus pour différents  séparés de 5 K. A titre de
comparaison, les profils théoriques dans le cas conductif -- obtenus
par la résolution de l'équation de la chaleur en géométrie
cylindrique -- sont aussi représentés. Nous commenterons ces
résultats en §
séparés de 5 K. A titre de
comparaison, les profils théoriques dans le cas conductif -- obtenus
par la résolution de l'équation de la chaleur en géométrie
cylindrique -- sont aussi représentés. Nous commenterons ces
résultats en § ![[*]](crossref.png) .
.
Figure:
Profils de température 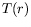 pour
pour 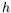 =1,9 mm.
A gauche : profils expérimentaux moyens.
A droite : profils conductifs théoriques.
Sur les deux graphes sont représentés les cas
=1,9 mm.
A gauche : profils expérimentaux moyens.
A droite : profils conductifs théoriques.
Sur les deux graphes sont représentés les cas
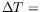 +15,
+10, +5, 0, -5, -10, -15 K.
+15,
+10, +5, 0, -5, -10, -15 K.
|
|
A partir des données précédentes, nous pouvons construire une
image représentant le champ de température dans toute une section
radiale 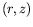 de la celulle. De telles images sont représentées
sur la figure
de la celulle. De telles images sont représentées
sur la figure ![[*]](crossref.png) . A côté de chaque image sont
présentés des profils verticaux de température déduits de ces
dernières. L'information ainsi extraite -- notament la stabilité
locale au sens de Rayleigh-Bénard -- est commentée en
§
. A côté de chaque image sont
présentés des profils verticaux de température déduits de ces
dernières. L'information ainsi extraite -- notament la stabilité
locale au sens de Rayleigh-Bénard -- est commentée en
§ ![[*]](crossref.png) .
.
Figure:
Images du champ de température et profils verticaux de température 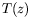 correspondants pour
correspondants pour 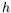 =1,9 mm,
=1,9 mm,
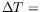 +5, +10, +15 K. Sur les images, le noir correspond à la
température la plus basse
+5, +10, +15 K. Sur les images, le noir correspond à la
température la plus basse
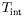 et le blanc à la plus chaude
et le blanc à la plus chaude
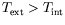 . Chacun des 12 profils de chaque graphe
est obtenu en moyennant 10 profils expérimentaux adjacents espacés
de 0.5 mm.
. Chacun des 12 profils de chaque graphe
est obtenu en moyennant 10 profils expérimentaux adjacents espacés
de 0.5 mm.
|
|
A titre indicatif, nous donnons ci-dessous les valeurs du gradient
« théorique »
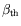 -- calculé brutalement en
divisant
-- calculé brutalement en
divisant  par
par
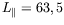 mm : c'est donc une valeur
« globale » -- ainsi que les valeurs du gradient effectif
mm : c'est donc une valeur
« globale » -- ainsi que les valeurs du gradient effectif
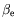 -- pente du profil expérimental de température
loin des bords de la cellule.
-- pente du profil expérimental de température
loin des bords de la cellule.
 |
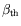 (mK/mm) (mK/mm) |
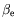 (mK/mm) (mK/mm) |
| 15 K |
236 |
76 |
| 10 K |
157 |
46 |
| 5 K |
79 |
25 |
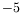 K K |
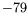 |
37 |
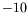 K K |
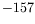 |
60 |
 K K |
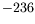 |
78 |
Le gradient effectif loin des bords est donc de 2 à 3 fois plus faible
que le gradient imposé « globalement » à la cellule.




suivant: 4.1.3 Hauteur de fluide
monter: 4.1 Profils de température
précédent: 4.1.1 Protocole
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) représente les différents profils
radiaux mesurés pour
représente les différents profils
radiaux mesurés pour
![\includegraphics[width=8cm]{h19t05al}](img940.png)
![\includegraphics[width=8cm]{h19t05me}](img941.png)
![[*]](crossref.png) présente alors les profils moyens
obtenus pour différents
présente alors les profils moyens
obtenus pour différents ![]() séparés de 5 K. A titre de
comparaison, les profils théoriques dans le cas conductif -- obtenus
par la résolution de l'équation de la chaleur en géométrie
cylindrique -- sont aussi représentés. Nous commenterons ces
résultats en §
séparés de 5 K. A titre de
comparaison, les profils théoriques dans le cas conductif -- obtenus
par la résolution de l'équation de la chaleur en géométrie
cylindrique -- sont aussi représentés. Nous commenterons ces
résultats en § ![[*]](crossref.png) .
.
![\includegraphics[width=8cm]{h19mean}](img944.png)
![\includegraphics[width=8cm]{conduct}](img945.png)
![]() de la celulle. De telles images sont représentées
sur la figure
de la celulle. De telles images sont représentées
sur la figure ![[*]](crossref.png) . A côté de chaque image sont
présentés des profils verticaux de température déduits de ces
dernières. L'information ainsi extraite -- notament la stabilité
locale au sens de Rayleigh-Bénard -- est commentée en
§
. A côté de chaque image sont
présentés des profils verticaux de température déduits de ces
dernières. L'information ainsi extraite -- notament la stabilité
locale au sens de Rayleigh-Bénard -- est commentée en
§ ![[*]](crossref.png) .
.
![]() -- calculé brutalement en
divisant
-- calculé brutalement en
divisant ![]() par
par
![]() mm : c'est donc une valeur
« globale » -- ainsi que les valeurs du gradient effectif
mm : c'est donc une valeur
« globale » -- ainsi que les valeurs du gradient effectif
![]() -- pente du profil expérimental de température
loin des bords de la cellule.
-- pente du profil expérimental de température
loin des bords de la cellule.