



suivant: 4.2.3 Cas des petites
monter: 4.2 Rouleaux corotatifs
précédent: 4.2.1 Présentation visuelle du
Table des matières
4.2.2 Présentation des mesures
Dans cette section, les ondes sont absentes ou nous ne nous en
préocupons pas : nous observons l'écoulement de base dans lequel
aucune brisure de symétrie n'intervient encore. Nous ne conservons que
les objets stationnaires de la structure convective. La symétrie de
révolution du problème nous permet de nous restreindre à un rayon
de la cellule pour décrire toute la structure spatiale. A partir d'un
cliché ombroscopique, nous représentons le signal dans le plan
orthogonal
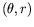 en dépliant l'image comme expliqué en
annexe
en dépliant l'image comme expliqué en
annexe ![[*]](crossref.png) . Nous procédons alors à un filtrage dans
la direction
. Nous procédons alors à un filtrage dans
la direction 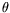 qui ne conserve que les modes 0 (moyenne) et 1
(éventuelle modulation due à un « décentrage » de la structure
et de l'origine des coordonnées cylindriques). Nous filtrons ensuite
dans la direction radiale autour du nombre d'onde moyen des rouleaux et
procédons à une transformation de Hilbert. Nous obtenons alors
l'amplitude locale et le nombre d'onde local de la structure en
rouleaux, que nous moyennons dans la direction
qui ne conserve que les modes 0 (moyenne) et 1
(éventuelle modulation due à un « décentrage » de la structure
et de l'origine des coordonnées cylindriques). Nous filtrons ensuite
dans la direction radiale autour du nombre d'onde moyen des rouleaux et
procédons à une transformation de Hilbert. Nous obtenons alors
l'amplitude locale et le nombre d'onde local de la structure en
rouleaux, que nous moyennons dans la direction 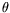 afin d'augmenter
le rapport signal/bruit.
afin d'augmenter
le rapport signal/bruit.
Afin d'avoir une meilleure résolution, notament dans le régime où
les ondes hydrothermales sont présentes, l'image que nous traitons est
parfois remplacée par la moyenne d'une série d'images acquises sur
un grand nombre de périodes des ondes hydrothermales : une telle image
moyenne ne contient ainsi plus l'information relative aux modes
oscillants. La fréquence d'acquisition des images est choisie autour
de 2 Hz, et plusieurs dizaines d'images sont moyennées. Les
figures ![[*]](crossref.png) ,
, ![[*]](crossref.png) et
et ![[*]](crossref.png) illustrent ce procédé sur des cas
typiques. Le même traitement que celui énoncé ci-dessus est
ensuite appliqué. Cela nous permet d'étudier les rouleaux
stationnaires dans un régime où ils sont partiellement recouverts
par les ondes. Cette démarche est complémentaire de celle qui
consiste à filtrer des diagrammes spatio-temporels dans la direction
temporelle pour éliminer les modes stationnaires.
illustrent ce procédé sur des cas
typiques. Le même traitement que celui énoncé ci-dessus est
ensuite appliqué. Cela nous permet d'étudier les rouleaux
stationnaires dans un régime où ils sont partiellement recouverts
par les ondes. Cette démarche est complémentaire de celle qui
consiste à filtrer des diagrammes spatio-temporels dans la direction
temporelle pour éliminer les modes stationnaires.
Les figures ![[*]](crossref.png) ,
respectivement
,
respectivement ![[*]](crossref.png) , présentent une succession de
profils d'amplitude locale obtenue par la méthode précedente pour
différentes valeurs de la différence de températures
, présentent une succession de
profils d'amplitude locale obtenue par la méthode précedente pour
différentes valeurs de la différence de températures
 ,
respectivement
,
respectivement
 . Sur tous les profils est observable une
forte variation de l'amplitude aux bords, ce qui n'a pas de sens
physique mais provient du filtrage dans la direction radiale ; cette
«pollution» numérique doit être écartée lors de la mesure de
l'amplitude moyenne. Dans le cas
. Sur tous les profils est observable une
forte variation de l'amplitude aux bords, ce qui n'a pas de sens
physique mais provient du filtrage dans la direction radiale ; cette
«pollution» numérique doit être écartée lors de la mesure de
l'amplitude moyenne. Dans le cas
 , nous pouvons néanmoins
mesurer une amplitude maximale réalisée à l'intérieur de la
cellule et qui a un sens ; ceci n'est plus vrai pour
, nous pouvons néanmoins
mesurer une amplitude maximale réalisée à l'intérieur de la
cellule et qui a un sens ; ceci n'est plus vrai pour
 .
.




suivant: 4.2.3 Cas des petites
monter: 4.2 Rouleaux corotatifs
précédent: 4.2.1 Présentation visuelle du
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ,
, ![[*]](crossref.png) et
et ![[*]](crossref.png) illustrent ce procédé sur des cas
typiques. Le même traitement que celui énoncé ci-dessus est
ensuite appliqué. Cela nous permet d'étudier les rouleaux
stationnaires dans un régime où ils sont partiellement recouverts
par les ondes. Cette démarche est complémentaire de celle qui
consiste à filtrer des diagrammes spatio-temporels dans la direction
temporelle pour éliminer les modes stationnaires.
illustrent ce procédé sur des cas
typiques. Le même traitement que celui énoncé ci-dessus est
ensuite appliqué. Cela nous permet d'étudier les rouleaux
stationnaires dans un régime où ils sont partiellement recouverts
par les ondes. Cette démarche est complémentaire de celle qui
consiste à filtrer des diagrammes spatio-temporels dans la direction
temporelle pour éliminer les modes stationnaires.