



suivant: C.2 Etats transitoires et
monter: C. Déterminations expérimentales des
précédent: C. Déterminations expérimentales des
Table des matières
C.1 Courbe de stabilité marginale dans l'anneau et relation de dispersion
Comme exposé en § ![[*]](crossref.png) , le nombre d'onde moyen dans
l'anneau est évidement discret et sa valeur au seuil
, le nombre d'onde moyen dans
l'anneau est évidement discret et sa valeur au seuil 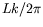 hésite entre 54 et 55. Après perturbation de ces états et/ou
réduction du paramètre de contrôle
hésite entre 54 et 55. Après perturbation de ces états et/ou
réduction du paramètre de contrôle  à partir d'états
excités de nombre d'onde différents, il est possible d'obtenir des
séries de valeurs de l'amplitude et de la fréquence en fonction de
à partir d'états
excités de nombre d'onde différents, il est possible d'obtenir des
séries de valeurs de l'amplitude et de la fréquence en fonction de
 pour une valeur entière du nombre d'onde moyen bien
déterminée. La figure
pour une valeur entière du nombre d'onde moyen bien
déterminée. La figure ![[*]](crossref.png) présente quelques une des
courbes obtenues pour l'amplitude. A partir de chaque série, nous en
déduisons la valeur critique de
présente quelques une des
courbes obtenues pour l'amplitude. A partir de chaque série, nous en
déduisons la valeur critique de  pour chaque valeur du
nombre d'onde. Cela nous donne accès à la courbe de stabilité
marginale (figure
pour chaque valeur du
nombre d'onde. Cela nous donne accès à la courbe de stabilité
marginale (figure ![[*]](crossref.png) ) qui par sa courbure au
voisinage du seuil nous donne la valeur de la longueur de cohérence
) qui par sa courbure au
voisinage du seuil nous donne la valeur de la longueur de cohérence
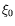 .
.
Figure:
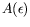 pour différents modes entiers
pour différents modes entiers 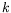 (
(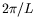 ).
Chaque graphe nous donne accès à la valeur du seuil
correspondant à un nombre d'onde, i.e. un point de la courbe
de stabilité marginale.
).
Chaque graphe nous donne accès à la valeur du seuil
correspondant à un nombre d'onde, i.e. un point de la courbe
de stabilité marginale.
|
|
Figure:
Courbe de stabilité marginale obtenue dans l'anneau.
Les cercles (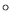 ) sont les valeurs des seuils déduites
des graphes de la figure
) sont les valeurs des seuils déduites
des graphes de la figure ![[*]](crossref.png) . Les points affublés
d'une grande barre d'erreur représente des séries ne contenant
que quelque points de mesure et n'ont pas été utilisé
pour l'ajustement. Les symboles (
. Les points affublés
d'une grande barre d'erreur représente des séries ne contenant
que quelque points de mesure et n'ont pas été utilisé
pour l'ajustement. Les symboles (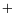 )
représentent pour chaque valeur du nombre d'onde les états
stables obtenus pour la plus faible valeur de
)
représentent pour chaque valeur du nombre d'onde les états
stables obtenus pour la plus faible valeur de  .
De même, les symboles (
.
De même, les symboles (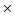 ) représentent les états
instables obtenus pour les valeurs les plus élevées de
) représentent les états
instables obtenus pour les valeurs les plus élevées de  .
La courbe en trait plein représente la meilleure approximation
des seuils (
.
La courbe en trait plein représente la meilleure approximation
des seuils ( ) et l'on en déduit la valeur de
) et l'on en déduit la valeur de 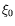 .
.
|
|
Figure:
Evolution de la fréquence
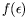 pour différents
modes entiers
pour différents
modes entiers 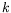 (
(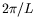 ).
).
|
|
En effectuant le même travail sur la fréquence en lieu et place de
l'amplitude, nous en déduisons la valeur de la vitesse de groupe
(dérivée première au seuil) ainsi que la valeur du facteur
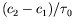 (courbure au seuil) ; les variations de la
fréquence en
(courbure au seuil) ; les variations de la
fréquence en  et
et 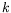 sont reproduites sur la
figure
sont reproduites sur la
figure ![[*]](crossref.png) .
.
Comme on peut le voir sur la figure ![[*]](crossref.png) , les différentes
courbes représentant l'amplitude en fonction de
, les différentes
courbes représentant l'amplitude en fonction de  n'ont pas
la même pente et la dépendance de l'amplitude
n'ont pas
la même pente et la dépendance de l'amplitude
 vis-à-vis du nombre d'onde ne peut se résumer à la simple relation
vis-à-vis du nombre d'onde ne peut se résumer à la simple relation
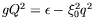 . En utilisant la modélisation
proposée en annexe
. En utilisant la modélisation
proposée en annexe ![[*]](crossref.png) , nous avons la relation plus
riche
, nous avons la relation plus
riche
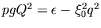 , où
, où
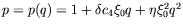 est une fonction de
est une fonction de 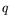 exprimée dans l'annexe
précédente. Nous ajustons donc la dépendance de l'amplitude
exprimée dans l'annexe
précédente. Nous ajustons donc la dépendance de l'amplitude 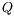 vis-à-vis de
vis-à-vis de  et
et 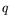 et obtenons globalement les valeurs des
coefficients du polynôme correspondant. La figure
et obtenons globalement les valeurs des
coefficients du polynôme correspondant. La figure ![[*]](crossref.png) représente alors le parfait alignement des points expérimentaux
après correction par les nouveaux termes de l'équation d'amplitude.
représente alors le parfait alignement des points expérimentaux
après correction par les nouveaux termes de l'équation d'amplitude.
Figure:
Graphe de l'amplitude corrigée
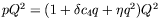 en fonction de l'écart au seuil corrigé
en fonction de l'écart au seuil corrigé
 pour
l'ensemble des nombres d'onde
pour
l'ensemble des nombres d'onde
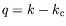 accessibles dans l'expérience. Les valeurs des coefficients
intervenant dans
accessibles dans l'expérience. Les valeurs des coefficients
intervenant dans 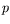 proviennent de l'ajustement global correspondant.
Après correction, l'ensemble des points se rassemble bien
le long d'une droite.
proviennent de l'ajustement global correspondant.
Après correction, l'ensemble des points se rassemble bien
le long d'une droite.
|
|
Les séries d'expériences requises pour construire le ballon de
stabilité ont été effectuées par Arnaud Prigent dans le cadre de
son stage de DEA.




suivant: C.2 Etats transitoires et
monter: C. Déterminations expérimentales des
précédent: C. Déterminations expérimentales des
Table des matières
Nicolas Garnier - Thèse de doctorat
![\includegraphics[width=16cm]{Ax8-eps}](img1256.png)
![[*]](crossref.png) , le nombre d'onde moyen dans
l'anneau est évidement discret et sa valeur au seuil
, le nombre d'onde moyen dans
l'anneau est évidement discret et sa valeur au seuil ![[*]](crossref.png) présente quelques une des
courbes obtenues pour l'amplitude. A partir de chaque série, nous en
déduisons la valeur critique de
présente quelques une des
courbes obtenues pour l'amplitude. A partir de chaque série, nous en
déduisons la valeur critique de ![[*]](crossref.png) ) qui par sa courbure au
voisinage du seuil nous donne la valeur de la longueur de cohérence
) qui par sa courbure au
voisinage du seuil nous donne la valeur de la longueur de cohérence
![\includegraphics[width=16cm]{Ax8-eps}](img1256.png)
![]() (courbure au seuil) ; les variations de la
fréquence en
(courbure au seuil) ; les variations de la
fréquence en ![]() et
et ![]() sont reproduites sur la
figure
sont reproduites sur la
figure ![[*]](crossref.png) .
.
![[*]](crossref.png) , les différentes
courbes représentant l'amplitude en fonction de
, les différentes
courbes représentant l'amplitude en fonction de ![]() n'ont pas
la même pente et la dépendance de l'amplitude
n'ont pas
la même pente et la dépendance de l'amplitude
![]() vis-à-vis du nombre d'onde ne peut se résumer à la simple relation
vis-à-vis du nombre d'onde ne peut se résumer à la simple relation
![]() . En utilisant la modélisation
proposée en annexe
. En utilisant la modélisation
proposée en annexe ![[*]](crossref.png) , nous avons la relation plus
riche
, nous avons la relation plus
riche
![]() , où
, où
![]() est une fonction de
est une fonction de ![]() exprimée dans l'annexe
précédente. Nous ajustons donc la dépendance de l'amplitude
exprimée dans l'annexe
précédente. Nous ajustons donc la dépendance de l'amplitude ![]() vis-à-vis de
vis-à-vis de ![]() et
et ![]() et obtenons globalement les valeurs des
coefficients du polynôme correspondant. La figure
et obtenons globalement les valeurs des
coefficients du polynôme correspondant. La figure ![[*]](crossref.png) représente alors le parfait alignement des points expérimentaux
après correction par les nouveaux termes de l'équation d'amplitude.
représente alors le parfait alignement des points expérimentaux
après correction par les nouveaux termes de l'équation d'amplitude.
![\includegraphics[width=12cm]{ampl-ren}](img1267.png)