1.3.5.1 Mécanisme pour

suivant: 1.3.5.2 Mécanisme pour monter: 1.3.5 Mécanismes heuristiques précédent: 1.3.5 Mécanismes heuristiques Table des matières

1.3.5.1 Mécanisme pour $\mathit P{\mathrm r}\xspace \rightarrow 0$

La chaleur diffuse plus vite que la quantité de mouvement donc les effets inertiels dominent. Le mécanisme décrit ci-après est très proche de celui de Pearson (1958) expliquant la convection stationnaire de Bénard-Marangoni ; il est juste modifié par l'existence d'un écoulement de base qui advecte en moyenne les cellules de Bénard.

**Figure:** Schéma illustrant une ligne chaude en surface du fluide et les mouvements induits par la présence de cette ligne. Pour des petits nombres de Prandtl, cette perturbation sera entretenue et se propagera suivant la vitesse en surface (voir texte).
$\includegraphics[width=8cm]{mecanism}$ $\begin{picture}(0,0)(0,0) \put( 165,122){\makebox(0,0)[r]{ligne plus chaude}} ... ...{$\vec{e}_\perp$}} \put( 132, 70){\makebox(0,0)[r]{$\vec{e}_z$}} \end{picture}$

Supposons une perturbation sous la forme d'une ligne plus chaude située à la surface et parallèle au gradient (figure

). Comme cette ligne est plus chaude, la tension de surface y est plus faible qu'à gauche et qu'à droite et le fluide s'écoule donc en surface à partir de la ligne et vers l'extérieur. Par conservation de la matière dans un voisinage de la ligne, nous en déduisons que le fluide est sous cette dernière animé d'un mouvement ascendant (voir figure). Or ce fluide qui remonte vers la surface est moins chaud, et moins rapide (cf. profils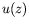

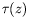et $\tau(z)$ de l'écoulement de base, Fig.

). Comme $\mathit P{\mathrm r}\xspace \rightarrow 0$ , le fluide est plus vite à l'équilibre thermique que mécanique et la ligne chaude se refroidit mais reste animée d'une vitesse plus faible que le reste de la surface. Cette vitesse plus faible refroidit encore la ligne qui se transforme par inertie en ligne froide. La tension de surface et la conservation de la matière opèrent alors en sens contraire pour enfoncer le fluide de la ligne et le remplacer ainsi par des particules plus chaudes et plus rapides provenant de la surface avoisinante de la ligne froide. La thermalisation opère et réchauffe la ligne mais par inertie celle-ci reste animée d'une vitesse plus rapide. Elle va donc continuer à se chauffer jusqu'à une température plus élevée que son voisinage lorsque l'équilibre mécanique sera atteint. Nous sommes ainsi revenus à la situation initiale -- une ligne chaude -- et une période des ondes s'est écoulée.

Ce mécanisme explique une propagation des ondes dans la direction du gradient, du froid vers le chaud. Remarquons qu'il est « saturé » au contraire du mécanisme proposé par Pearson, et qu'il est ainsi susceptible de s'éteindre de lui-même...

suivant: 1.3.5.2 Mécanisme pour monter: 1.3.5 Mécanismes heuristiques précédent: 1.3.5 Mécanismes heuristiques Table des matières

Nicolas Garnier - Thèse de doctorat