



suivant: 4. Ecoulement de base
monter: 3. Transition convectif/absolu pour
précédent: 3.2.3.5 e. Mesures des
Table des matières
A priori, si la vitesse de groupe 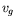 ne s'annule pas, les
instabilités d'ordre supérieur pouvant intervenir sont convectives
au voisinage de leur seuil. Deissler a ainsi observé numériquement
une turbulence faible advectée dans l'équation de
ne s'annule pas, les
instabilités d'ordre supérieur pouvant intervenir sont convectives
au voisinage de leur seuil. Deissler a ainsi observé numériquement
une turbulence faible advectée dans l'équation de
 GL avec
vitesse de groupe ; et les sillages regorgent d'exemple de ce type.
GL avec
vitesse de groupe ; et les sillages regorgent d'exemple de ce type.
Dans le cas de l'anneau, les conditions aux limites périodiques
empêchent à priori cette phénoménologie. Néanmoins, nous
pouvons imaginer que dans le cas où existent des couples {puits,
source}, les régions d'onde droite et les régions d'onde gauche
soient suffisamment séparées pour se comporter comme des « petites
boîtes finies », au moins sur des temps 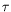 courts, i.e.,
petits devant les temps caractéristiques de déplacement des sources
et des puits. Un tel régime suppose bien sûr que ces objets ne se
déplacent quasiment pas sur une période de l'onde de base, ce qui
est plutôt un cas assez rare parmi tous les régimes à fort
courts, i.e.,
petits devant les temps caractéristiques de déplacement des sources
et des puits. Un tel régime suppose bien sûr que ces objets ne se
déplacent quasiment pas sur une période de l'onde de base, ce qui
est plutôt un cas assez rare parmi tous les régimes à fort
 observés dans l'anneau. En résumé, des effets
attachés à la transition convectif/absolu sont donc envisageables
dans l'anneau lorsque des couples {puits, source} existent ; nous
pouvons ainsi imaginer que l'expérience de Lega et al. (1992) -- où des
dislocations sont observées -- est dans ce cas. Coullet et al. (1993) ont
par ailleurs montré que la stabilité des sources est directement
liée au caractère convectif ou absolu de la stabilité des
solutions ondes planes que ces objets permettent de « raccorder ».
observés dans l'anneau. En résumé, des effets
attachés à la transition convectif/absolu sont donc envisageables
dans l'anneau lorsque des couples {puits, source} existent ; nous
pouvons ainsi imaginer que l'expérience de Lega et al. (1992) -- où des
dislocations sont observées -- est dans ce cas. Coullet et al. (1993) ont
par ailleurs montré que la stabilité des sources est directement
liée au caractère convectif ou absolu de la stabilité des
solutions ondes planes que ces objets permettent de « raccorder ».
Dans le rectangle, le mode 17 devient à son tour instable d'Eckhaus
pour
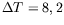 K (
K (
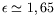 ). A priori, nous pouvons
attendre la même phénoménologie que celle observée pour
l'instabilité d'Eckhaus du mode 21. Celui-ci n'est d'ailleurs plus
observé et la source émet directement le mode 17 modulé. La
figure
). A priori, nous pouvons
attendre la même phénoménologie que celle observée pour
l'instabilité d'Eckhaus du mode 21. Celui-ci n'est d'ailleurs plus
observé et la source émet directement le mode 17 modulé. La
figure ![[*]](crossref.png) illustre, dans le cas où le mode 17 est
absolument instable, le régime transitoire menant au régime
stationnaire après une augmentation de
illustre, dans le cas où le mode 17 est
absolument instable, le régime transitoire menant au régime
stationnaire après une augmentation de  . Nous y voyons ainsi
la naissance des modulations, puis leur éclatement en un front de
dislocations. Ce front naît sur le bord aval (à droite) à la
date
. Nous y voyons ainsi
la naissance des modulations, puis leur éclatement en un front de
dislocations. Ce front naît sur le bord aval (à droite) à la
date
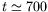 s et se déplace ensuite à contre-courant
jusqu`à atteindre sa position d'équilibre en
s et se déplace ensuite à contre-courant
jusqu`à atteindre sa position d'équilibre en
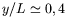 . Cette
dynamique est exactement la même que celle des transitoires observés
à l'établissement du régime d'instabilité d'Eckhaus absolue du
mode 21. Néanmoins, le diagramme de la figure
. Cette
dynamique est exactement la même que celle des transitoires observés
à l'établissement du régime d'instabilité d'Eckhaus absolue du
mode 21. Néanmoins, le diagramme de la figure ![[*]](crossref.png) présente en plus un autre phénomène. En aval du premier front, des
modulations existent qui sont à leur tour amplifiées jusqu'à
conduire à de nouvelles dislocations à partir de
présente en plus un autre phénomène. En aval du premier front, des
modulations existent qui sont à leur tour amplifiées jusqu'à
conduire à de nouvelles dislocations à partir de
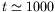 s.
Ces dislocations forment un second front qui se propage à son tour à
rebrousse-poil. Un fait remarquable est que ces dislocations se
produisent très régulièrement avec une période qui est
exactement le double de la période des dislocations du premier front.
Non content de cela, le système nous offre alors suivant le même
principe l'apparition en aval d'une nouvelle fréquence de modulations,
suivies d'un nouveau front de dislocations, de période encore
doublée (soit 4 fois la période initiale). En fin de fichier
-- malheureusement trop court -- un nouveau doublement de période
survient (dislocations à 8 fois la période initiale).
s.
Ces dislocations forment un second front qui se propage à son tour à
rebrousse-poil. Un fait remarquable est que ces dislocations se
produisent très régulièrement avec une période qui est
exactement le double de la période des dislocations du premier front.
Non content de cela, le système nous offre alors suivant le même
principe l'apparition en aval d'une nouvelle fréquence de modulations,
suivies d'un nouveau front de dislocations, de période encore
doublée (soit 4 fois la période initiale). En fin de fichier
-- malheureusement trop court -- un nouveau doublement de période
survient (dislocations à 8 fois la période initiale).
Figure:
Diagramme spatio-temporel pour  =8,5 K, illustrant
une cascade temporelle de doublement de période
dans un régime transitoire menant à un état où
le second mode (17) est à son tour instable d'Eckhaus
(absolument).
=8,5 K, illustrant
une cascade temporelle de doublement de période
dans un régime transitoire menant à un état où
le second mode (17) est à son tour instable d'Eckhaus
(absolument).
|
|




suivant: 4. Ecoulement de base
monter: 3. Transition convectif/absolu pour
précédent: 3.2.3.5 e. Mesures des
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png)
![\includegraphics[width=8cm]{a06d1kx}](img924.png)