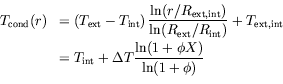
![[*]](crossref.png) et
et ![[*]](crossref.png) , les profils radiaux moyens de température sont
très éloignés des profils conductifs logarithmiques solutions de
l'équation de la chaleur en géométrie cylindrique :
, les profils radiaux moyens de température sont
très éloignés des profils conductifs logarithmiques solutions de
l'équation de la chaleur en géométrie cylindrique :
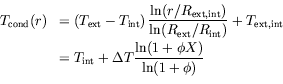
Hors de ces deux zones aux extrémités du domaine, la distribution de
température n'est pas logarithmique et le gradient n'est ainsi pas
hyperbolique. Au contraire, les mesures expérimentales suggèrent que
ce gradient effectif est quasiment constant loin des bords de la
cellule. Les effets consécutifs à la géométrie cylindrique et
à l'existence d'un point singulier en ![]() sont ainsi complètement
masqués pour le champ de température dans l'écoulement de base.
sont ainsi complètement
masqués pour le champ de température dans l'écoulement de base.
Comment expliquer cette linéarité du profil radial de
température ? Celle-ci est reliée à l'existence d'une couche
limite autour du plot central, qui absorbe une grande partie de la
différence de température imposée. Cette couche limite peut
résulter d'une évaporation relativement plus importante dans la
région centrale, ainsi que d'un rayonnement lui aussi plus accentué
par la géométrie cylindrique. De plus, la différence de
température est imposée dans un demi-espace seulement : le plot
central et la couronne en cuivre imposent au miroir constituant le fond
de la cellule une distribution radiale de température qui est très
proche de la distribution conductive théorique énoncée ci-dessus.
Par contre, le plot central et la couronne en cuivre ne peuvent imposer
un gradient conductif à la couche d'air située sur la surface libre
du fluide. Comme l'évoque le schéma de la
figure ![[*]](crossref.png) , une déformation importante des
isothermes dans l'air peut se ressentir sur les isothermes dans le
fluide. De tels effets existent sans doute dans notre expérience.
, une déformation importante des
isothermes dans l'air peut se ressentir sur les isothermes dans le
fluide. De tels effets existent sans doute dans notre expérience.
![\includegraphics[width=15cm]{isotherm}](img971.png)
|
Remarquons enfin que la linéarité du profil de température est
observée pour les deux hauteurs ![]() =1,2 mm et
=1,2 mm et ![]() =1,9 mm ; mais
qu'elle est plus nette pour les grandes hauteurs.
=1,9 mm ; mais
qu'elle est plus nette pour les grandes hauteurs.