



suivant: 4.1.4.3 Une distribution verticale
monter: 4.1.4 Analyse des résultats
précédent: 4.1.4.1 Une distribution radiale
Table des matières
Commençons tout d'abord par le constat suivant : pour 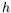 =1,2 mm les
profils verticaux de température sont difficiles à isoler du bruit
qui entoure les mesures. Cela signifie néanmoins que ces profils sont
peu marqués (
=1,2 mm les
profils verticaux de température sont difficiles à isoler du bruit
qui entoure les mesures. Cela signifie néanmoins que ces profils sont
peu marqués (
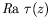 est d'amplitude faible) et nous avons pu
constater que les ondes hydrothermales ont une amplitude en
température de l'ordre de l'amplitude du profil vertical de
température. Pour cela, nous avons réalisé des expériences
complémentaires en mesurant le signal temporel en un point de la
cellule et en répétant l'opération sur une série de points
alignés verticalement. La figure
est d'amplitude faible) et nous avons pu
constater que les ondes hydrothermales ont une amplitude en
température de l'ordre de l'amplitude du profil vertical de
température. Pour cela, nous avons réalisé des expériences
complémentaires en mesurant le signal temporel en un point de la
cellule et en répétant l'opération sur une série de points
alignés verticalement. La figure ![[*]](crossref.png) représente
alors pour chaque série temporelle la valeur moyenne, ainsi que les
extrema ce qui donne l'amplitude en température des ondes
hydrothermales. Cette dernière est du même ordre que la différence
des températures entre
représente
alors pour chaque série temporelle la valeur moyenne, ainsi que les
extrema ce qui donne l'amplitude en température des ondes
hydrothermales. Cette dernière est du même ordre que la différence
des températures entre 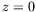 et
et 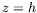 . On s'attend à ce que cette
différence évolue proportionnellement à
. On s'attend à ce que cette
différence évolue proportionnellement à  (§
(§ ![[*]](crossref.png) , éq. (
, éq. (![[*]](crossref.png) )
p.
)
p. ![[*]](crossref.png) ) alors que l'amplitude des ondes suit une loi
en racine carrée avant de saturer (cf §
) alors que l'amplitude des ondes suit une loi
en racine carrée avant de saturer (cf § ![[*]](crossref.png) ).
).
Notons que la figure ![[*]](crossref.png) illustre clairement que les
ondes hydrothermales sont -- entre autres composantes -- des ondes de
température en volume.
illustre clairement que les
ondes hydrothermales sont -- entre autres composantes -- des ondes de
température en volume.
Figure:
Profil vertical de la température moyenne (ligne continue et points 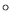 ),
minimale et maximale (lignes continues sans point)
en présence d'ondes hydrothermales, pour
),
minimale et maximale (lignes continues sans point)
en présence d'ondes hydrothermales, pour 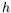 =1,2 mm,
=1,2 mm,
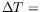 15 K
et à la position
15 K
et à la position 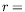 17,5 mm.
17,5 mm.
|
|




suivant: 4.1.4.3 Une distribution verticale
monter: 4.1.4 Analyse des résultats
précédent: 4.1.4.1 Une distribution radiale
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) illustre clairement que les
ondes hydrothermales sont -- entre autres composantes -- des ondes de
température en volume.
illustre clairement que les
ondes hydrothermales sont -- entre autres composantes -- des ondes de
température en volume.
![[*]](crossref.png) représente
alors pour chaque série temporelle la valeur moyenne, ainsi que les
extrema ce qui donne l'amplitude en température des ondes
hydrothermales. Cette dernière est du même ordre que la différence
des températures entre
représente
alors pour chaque série temporelle la valeur moyenne, ainsi que les
extrema ce qui donne l'amplitude en température des ondes
hydrothermales. Cette dernière est du même ordre que la différence
des températures entre ![[*]](crossref.png) , éq. (
, éq. (![[*]](crossref.png) )
p.
)
p. ![[*]](crossref.png) ) alors que l'amplitude des ondes suit une loi
en racine carrée avant de saturer (cf §
) alors que l'amplitude des ondes suit une loi
en racine carrée avant de saturer (cf § ![[*]](crossref.png) ).
).
![[*]](crossref.png) illustre clairement que les
ondes hydrothermales sont -- entre autres composantes -- des ondes de
température en volume.
illustre clairement que les
ondes hydrothermales sont -- entre autres composantes -- des ondes de
température en volume.
![\includegraphics[width=8cm]{ondes-v}](img974.png)