1.3.1 Historique

La première analyse de stabilité linéaire de l'écoulement de base a été effectuée par Smith et Davis (1983a) dans le cas rectangulaire purement thermocapillaire ( 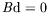$\mathit B{\mathrm d}\xspace = 0$) et en géométrie infinie. Cette étude a ensuite été complétée par la prise en compte des effets thermogravitaires à nombre de Prandtl bas, modéré et grands par Gershuni et al. (1992) et Parmentier et al. (1993). L'introduction d'un nombre de Biot par Mercier et Normand (1996) a permis de clarifier l'existence d'instabilités stationnaires associées à un gradient vertical de température instable au sens de Rayleigh-Bénard. Priede et Gerbeth (1997b) ont dans le même temps étudié en détail l'influence des différentes conditions aux limites thermiques dans le cas purement thermocapillaire. Priede et Gerbeth (1997a) ont enfin pris en compte le caractère convectif au seuil de l'instabilité en ondes, et déterminé le seuil du mode global dans le cas d'une boîte de taille finie. Les tableaux des figures  et résument les différentes études théoriques de stabilité linéaire dans les cas d'une géométrie infinie et d'une géométrie finie dans la direction du gradient de température.

Le cas de la géométrie cylindrique a été abordé par Vrane et Smith (1996), en autorisant des déflections de la surface libre, mais seules des perturbations de très grande longueur d'onde -- nombre d'onde azimuthal proche de l'unité -- ont été considérées. Nous présentons donc ici nos calculs de stabilité linéaire de l'écoulement de base en géométrie cylindrique.

Notons que nous avons jusqu'à présent négligé les déflections de surface dans le calcul de l'écoulement de base : nous avons supposé que la surface libre était indéformable. Tout comme Smith et Davis (1983a), nous poursuivons cette approche et les perturbations de l'écoulement de base que nous allons considérer ne contiennent pas de déflections de surface. Nous pouvons bien sûr imaginer un calcul plus complet où apparaîtraient de petites variations d'altitude de la surface, mais les ondes hydrothermales telles que décrites par Smith et Davis (1983a) ne nécessitent pas ce raffinement ; stricto sensu, les ondes hydrothermales ne sont même pas liées à des ondes de déformation de la surface libre. Cela va un peu à l'encontre de l'intuition que l'on peut avoir des ondes dans un système avec surface libre, et c'est sans doute pour cela que Smith et Davis (1983b) ont étudié le cas d'une interface déformée dans un second article concommitant. Une nouvelle instabilité oscillante associée à des ondes de surface a ainsi été mise en évidence, mais lors d'une étude n'impliquant qu'une dimension d'espace horizontale -- la direction du gradient --. Smith et Davis (1983b) montrent que cette instabilité ne devient plus dangereuse que les ondes hydrothermales que pour des faibles valeurs du nombre de Prandtl (typiquement 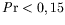$\mathit P{\mathrm r}\xspace <0,15$) mais précisent alors qu'un plus grand rapport d'aspect $\Gamma_\parallel$ abaisse le seuil de ces ondes de surface. Vu le nombre de Prandtl du fluide que nous utilisons, nous ne nous intéressons pas dans la suite aux ondes de surface non-hydrothermales, et négligeons les déflections de surface dans tous nos calculs. Expérimentalement toutefois, nous ne pouvons pas affirmer que les ondes hydrothermales ne sont pas couplées à des variations de l'altitude de la surface libre, mais il est clair que si cela est le cas, ce n'est pas le mécanisme ou la caractéristique principale des ondes que nous observons ; nous quantifions et discutons ces effets en § .